题目内容
△ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B等于( )
| A、70° |
| B、20°或70° |
| C、40°或70° |
| D、40°或20° |
考点:线段垂直平分线的性质,等腰三角形的性质
专题:分类讨论
分析:由于△ABC的形状不能确定,故应分△ABC是锐角三角形与钝角三角形两种情况进行讨论.
解答: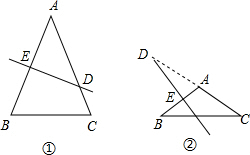 解:如图①,当AB的中垂线与线段AC相交时,则可得∠ADE=50°,
解:如图①,当AB的中垂线与线段AC相交时,则可得∠ADE=50°,
∵∠AED=90°,
∴∠A=90°-50°=40°,
∵AB=AC,
∴∠B=∠C=
=70°;
如图②,当AB的中垂线与线段CA的延长线相交时,则可得∠ADE=50°,
∵∠AED=90°,
∴∠DAE=90°-50°=40°,
∴∠BAC=140°,
∵AB=AC,
∴∠B=∠C=
=20°.
∴底角B为70°或20°.
故选:B.
 解:如图①,当AB的中垂线与线段AC相交时,则可得∠ADE=50°,
解:如图①,当AB的中垂线与线段AC相交时,则可得∠ADE=50°,∵∠AED=90°,
∴∠A=90°-50°=40°,
∵AB=AC,
∴∠B=∠C=
| 180°-∠A |
| 2 |
如图②,当AB的中垂线与线段CA的延长线相交时,则可得∠ADE=50°,
∵∠AED=90°,
∴∠DAE=90°-50°=40°,
∴∠BAC=140°,
∵AB=AC,
∴∠B=∠C=
| 180°-∠A |
| 2 |
∴底角B为70°或20°.
故选:B.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
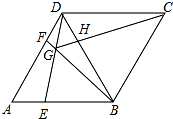 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )| A、只有①② | B、①②③ |
| C、只有②③ | D、只有①③ |
 如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )| A、∠B=∠E,BC=EF |
| B、∠A=∠D,BC=EF |
| C、∠A=∠D,∠B=∠E |
| D、BC=EF,AC=DF |
某果园2012年水果产量为100吨,2014年水果产量为144吨,则该果园水果产量的年平均增长率为多少?若设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
| A、144(1-x)2=100 |
| B、100(1-x)2=144 |
| C、144(1+x)2=100 |
| D、100(1+x)2=144 |
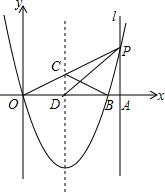 直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.
直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.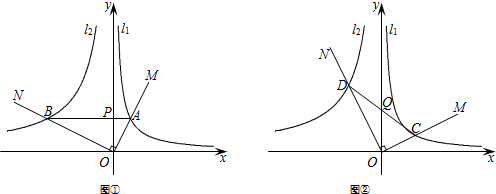
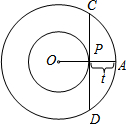 如图,已知OA=4cm,一个动点P从A向O以1cm/秒的速度运动,以O为圆心,分别以OA、OP为半径画大圆和小圆,以P为切点的小圆的切线与大圆交于C、D,则弦CD的长y(cm)关于P的运动时间t(秒)的函数解析式为
如图,已知OA=4cm,一个动点P从A向O以1cm/秒的速度运动,以O为圆心,分别以OA、OP为半径画大圆和小圆,以P为切点的小圆的切线与大圆交于C、D,则弦CD的长y(cm)关于P的运动时间t(秒)的函数解析式为