题目内容
17. 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )| A. | 8+6$\sqrt{3}$ | B. | 12$\sqrt{3}$ | C. | 19.2 | D. | 20 |
分析 利用翻折变换的性质得出四边形EFGH是矩形,进而得出BF=DH=MF,再利用勾股定理得出BE,BF的长,进而得出答案.
解答 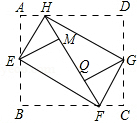 解:如图所示:设HF上两个点分别为M、Q,
解:如图所示:设HF上两个点分别为M、Q,
∵M点是B点对折过去的,
∴∠EMH为直角,△AEH≌△MEH,
∴∠HEA=∠MEH,
同理∠MEF=∠BEF,
∴∠MEH+∠MEF=90°,
∴四边形EFGH是矩形,
∴△DHG≌△BFE,△HEF是直角三角形,
∴BF=DH=MF,
∵AH=HM,
∴AD=HF,
∵EH=12,EF=16,
∴FH=$\sqrt{E{H}^{2}+E{F}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,
∴AE=EM=$\frac{EH×EF}{FH}$=$\frac{12×16}{20}$=$\frac{48}{5}$,
则BF=NF=$\sqrt{E{F}^{2}-E{M}^{2}}$=12.8,
故BE=$\sqrt{E{F}^{2}-B{F}^{2}}$=9.6,
∴AB=AE+BE=9.6+$\frac{48}{5}$=19.2.
故选:C.
点评 此题主要考查了翻折变换的性质以及勾股定理、矩形的判定方法等知识,根据题意得出AE,BE的长是解题关键.

练习册系列答案
相关题目
7. 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k3>k1 | C. | k3>k2>k1 | D. | k3>k1>k2 |
8.函数y=$\frac{x}{2}$的图象是( )
| A. | 双曲线 | B. | 抛物线 | C. | 直线 | D. | 线段 |
5.函数y=$\sqrt{x}$中的自变量x的取值范围是( )
| A. | x≥0 | B. | x≤0 | C. | x>0 | D. | x=0 |
2.抛物线y=-3x2+2x-l的图象与坐标轴交点的个数是( )
| A. | 没有交点 | B. | 只有一个交点 | C. | 两个交点 | D. | 三个交点 |
9.下列各式中正确的是( )
| A. | (a+4)(a-4)=a2-4 | B. | (5x-1)(1-5x)=25x2-1 | ||
| C. | (-3x+2)2=4-12x+9x2 | D. | (x-3)(x-9)=x2-27 |
6. 如图AB∥CD,∠BAE=120°,∠EDC=45°,则∠E=( )
如图AB∥CD,∠BAE=120°,∠EDC=45°,则∠E=( )
 如图AB∥CD,∠BAE=120°,∠EDC=45°,则∠E=( )
如图AB∥CD,∠BAE=120°,∠EDC=45°,则∠E=( )| A. | 105° | B. | 115° | C. | 120° | D. | 165° |
 如图所示的几何体是由一个正方体切去一个小正方形成的,从左面看到的平面图形为( )
如图所示的几何体是由一个正方体切去一个小正方形成的,从左面看到的平面图形为( )



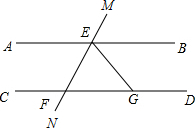 如图,直线AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠BEF,交CD于点G,若∠EFG=72°,求∠MEG的度数.
如图,直线AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠BEF,交CD于点G,若∠EFG=72°,求∠MEG的度数.