题目内容
2．已知抛物线y=x2-x-1与x轴的一个交点为（a，0），那么代数式a2-a+2016的值为2017．分析 把点的坐标代入函数解析式，求出a2-a=1，代入求出即可．
解答 解：∵抛物线y=x2-x-1与x轴的一个交点为（a，0），
∴代入得：a2-a-1=0，
∴a2-a=1，
∴a2-a+2016=1+2016=2017，
故答案为：2017．
点评 本题考查了抛物线与x轴的交点的应用，能求出a2-a=1是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．已知直线a∥b，点M到直线a的距离是5cm，到直线b的距离是3cm，那么直线a和b之间的距离是（ ）
| A． | 2cm | B． | 6cm | C． | 8cm | D． | 2cm或8cm |
13．如图所示，下列几何体中，主视图、左视图、俯视图都相同的是（ ）
| A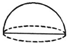． |  半球 | B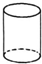． |  圆柱 | C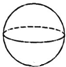． |  球 | D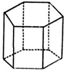． |  六棱柱 |
10．下列问题中，两个变量成正比例关系的是（ ）
| A． | 弧长确定，它所对的中心角和半径 | |
| B． | 长方形的长确定，它的周长与宽 | |
| C． | 扇形的中心角确定，它的面积与半径 | |
| D． | 正多边形边数确定，它的周长与边长 |
7．
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$，y=$\frac{{k}_{2}}{x}$，y=$\frac{{k}_{3}}{x}$在x轴上方的图象，由此观察k1，k2，k3的大小关系为（ ）
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$，y=$\frac{{k}_{2}}{x}$，y=$\frac{{k}_{3}}{x}$在x轴上方的图象，由此观察k1，k2，k3的大小关系为（ ）| A． | k1＞k2＞k3 | B． | k2＞k3＞k1 | C． | k3＞k2＞k1 | D． | k3＞k1＞k2 |
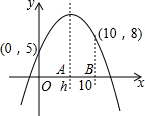如图，已知二次函数y=a（x-h）2+k在坐标平面上的图象经过（0，5）、（10，8）两点．若a＜0，0＜h＜10，则h的值可能为（ ）
如图所示的几何体是由一个正方体切去一个小正方形成的，从左面看到的平面图形为（ ）
