题目内容
19.已知点P(a+1,2a-1)关于x轴的对称点在第一象限,则a的取值范围是( )| A. | a>-1 | B. | a<$\frac{1}{2}$ | C. | -1$<a<\frac{1}{2}$ | D. | -1$≤a≤\frac{1}{2}$ |
分析 首先得出点P(a+1,2a-1)关于x轴的对称点(a+1,1-2a),进而求出a的取值范围.
解答 解:∵点P(a+1,2a-1)关于x轴的对称点为(a+1,1-2a),
∴$\left\{\begin{array}{l}{a+1>0}\\{1-2a>0}\end{array}\right.$,
∴解得:-1<a<$\frac{1}{2}$.
故选:C.
点评 此题主要考查了关于x轴对称点的性质以及一元一次不等式组的解法,正确得出关于a的不等式组是解题关键.

练习册系列答案
相关题目
9.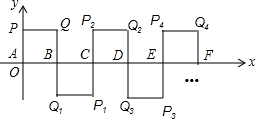 如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
 如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )| A. | (2016,1) | B. | (2015,1) | C. | (2016,-1) | D. | (4032,1) |
10.下列问题中,两个变量成正比例关系的是( )
| A. | 弧长确定,它所对的中心角和半径 | |
| B. | 长方形的长确定,它的周长与宽 | |
| C. | 扇形的中心角确定,它的面积与半径 | |
| D. | 正多边形边数确定,它的周长与边长 |
7. 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k3>k1 | C. | k3>k2>k1 | D. | k3>k1>k2 |
4.已知A(x1,y1)、B(x2,y2)和C(x3,y3)在直线y=-$\frac{1}{2}$x+$\sqrt{3}$上.若x1<x2<x3,下列判断正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
8.函数y=$\frac{x}{2}$的图象是( )
| A. | 双曲线 | B. | 抛物线 | C. | 直线 | D. | 线段 |
9.下列各式中正确的是( )
| A. | (a+4)(a-4)=a2-4 | B. | (5x-1)(1-5x)=25x2-1 | ||
| C. | (-3x+2)2=4-12x+9x2 | D. | (x-3)(x-9)=x2-27 |
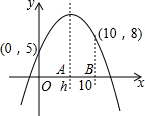 如图,已知二次函数y=a(x-h)2+k在坐标平面上的图象经过(0,5)、(10,8)两点.若a<0,0<h<10,则h的值可能为( )
如图,已知二次函数y=a(x-h)2+k在坐标平面上的图象经过(0,5)、(10,8)两点.若a<0,0<h<10,则h的值可能为( )