题目内容
19.先化简,再求值:(1)5(3x2y-xy2)-(xy2+3x2y),其中x=2,y=3.
(2)3x2y-[2x2y-3(2xy-x2y)-xy],其中x=-1,y是-$\frac{1}{2}$的倒数.
分析 (1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;
(2)原式去括号合并得到最简结果,求出y的值,再将x与y的值代入计算即可求出值.
解答 解:(1)原式=15x2y-5xy2-xy2-3x2y=12x2y-6xy2,
当x=2,y=3时,原式=12×22×3-6×2×32=36;
(2)原式=3x2y-(2x2y-6xy+3x2y-xy)=3x2y-5x2y+7xy=-3x2y+7xy,
∵x=-1,y是-$\frac{1}{2}$的倒数,
∴x=-1,y=-2,
则原式=-3×(-1)2×(-2)+7×(-1)×(-2)=20.
点评 此题考查了整式的加减-化简求值,熟练掌握去括号法则与合并同类项法则是解本题的关键.

练习册系列答案
相关题目
20.已知二次函数y=-(x-h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为-5,则h的值为( )
| A. | 3-$\sqrt{6}$或1+$\sqrt{6}$ | B. | 3-$\sqrt{6}$或3+$\sqrt{6}$ | C. | 3+$\sqrt{6}$或1-$\sqrt{6}$ | D. | 1-$\sqrt{6}$或1+$\sqrt{6}$ |
10.对于正比例函数y=2x,下列判断正确的是( )
| A. | 自变量x的值毎增加1,函数y的值增加2 | |
| B. | 自变量x的值毎增加1,函数y的值减少2 | |
| C. | 自变量x的值毎增加1,函数y的值增加$\frac{1}{2}$ | |
| D. | 自变量x的值毎增加1,函数y的值减少$\frac{1}{2}$ |
14.下列表格是二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0),a,b,c为常数)的一个解x的范围是( )
| x | 4.18 | 4.19 | 4.20 | 4.21 |
| y=ax2+bx+c | -0.0676 | -0.0139 | 0.04 | 0.0941 |
| A. | 4<x<4.18 | B. | 4.18<x<4.19 | C. | 4.19<x<4.20 | D. | 4.20<x<4.21 |
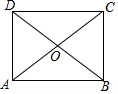 如图,在矩形ABCD中,对角线AC、BD相交于点O,且OA=OD.若∠OAD=50°,求∠OAB的度数.
如图,在矩形ABCD中,对角线AC、BD相交于点O,且OA=OD.若∠OAD=50°,求∠OAB的度数.