题目内容

4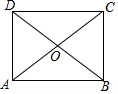．如图，在矩形ABCD中，对角线AC、BD相交于点O，且OA=OD．若∠OAD=50°，求∠OAB的度数．

分析 根据矩形的性质求出∠DAB，代入∠OAB=∠DAB-∠OAD求出即可．

解答 解：∵四边形ABCD是矩形，
∴∠DAB=90°，
∵∠OAD=50°，
∴∠OAB=∠DAB-∠OAD=40°

点评 本题考查了矩形的性质，能根据矩形的性质求出∠DAB的度数是解此题的关键．

练习册系列答案
相关题目
5．若m、n是一元二次方程x2-3x-1=0的两根，则m（n-1）-n的值为（　　）
A．-2B．2C．-4D．4
15．如图，一段抛物线：y=-x（x-2）（0≤x≤2）记为C1，它与x轴交于两点O、A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，直至得到C7，若点P（13，m）在第7段抛物线C7上，则m=1．
12．“齐天大圣”孙悟空有一个宝贝--金箍棒，当他快速旋转金箍棒时，展现在我们眼前的是一个圆的形象，这说明线动成面．
19．先化简，再求值：
（1）5（3x2y-xy2）-（xy2+3x2y），其中x=2，y=3．
（2）3x2y-[2x2y-3（2xy-x2y）-xy]，其中x=-1，y是-$\frac{1}{2}$的倒数．
9．我们知道：分式和分数有着很多的相似点．如类比分数的基本性质，我们得到了分式的基本性质；类比分数的运算法则，我们得到了分式的运算法则，等等．小学里，把分子比分母小的分数叫做真分数．类似地，我们把分子整式的次数小于分母整式的次数的分式称为真分式；反之，称为假分式．对于任何一个假分式都可以化成整式与真分式的和的形式，
如：$\frac{x+1}{x-1}$=$\frac{x-1+2}{x-1}$=$\frac{x-1}{x-1}$+$\frac{2}{x-1}$=1+$\frac{2}{x-1}$；
$\frac{2x-3}{x+1}$=$\frac{2x+2-5}{x+1}$=$\frac{2x+2}{x+1}$+$\frac{-5}{x+1}$=2+（-$\frac{5}{x-1}$）．
（1）下列分式中，属于真分式的是：③（填序号）；
①$\frac{a-2}{a+1}$　　     ②$\frac{{x}^{2}}{x+1}$        ③$\frac{2b}{{b}^{2}+3}$　    　④$\frac{{a}^{2}+3}{{a}^{2}-1}$
（2）将假分式$\frac{4a+3}{2a-1}$化成整式与真分式的和的形式为：$\frac{4a+3}{2a-1}$=2+$\frac{5}{2a-1}$，若假分式$\frac{4a+3}{2a-1}$的值为正整数，则整数a的值为-2、1或3；
（3）将假分式$\frac{{a}^{2}+3}{a-1}$ 化成整式与真分式的和的形式：$\frac{{a}^{2}+3}{a-1}$=a+1+$\frac{4}{a-1}$．
16．四个图形是如图所示正方体的展开图的是（　　）
A．B．C．D．
13．已知变量y与x的关系满足下表，那么能反映y与x之间的函数关系的解析式是（　　）
 x …-2 -10  12  …
 y… 43  21  0…
A．y=-2xB．y=x+4C．y=-x+2D．y=2x-2
14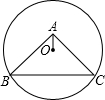．如图，⊙O过点B、C，圆心O在等腰直角△ABC的内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（　　）
A．2$\sqrt{3}$B．$\sqrt{13}$C．4D．3$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网