题目内容
7.先化简再求值($\frac{x+2}{x-2}$+$\frac{4}{{x}^{2}-4x+4}$)÷$\frac{x}{x-2}$,请从-2,-1,0,1,2中选一个x的值代入.分析 先化简题目中的式子,然后在题目中选取一个使得原分式有意义的值代入化简后的式子即可解答本题.
解答 解:($\frac{x+2}{x-2}$+$\frac{4}{{x}^{2}-4x+4}$)÷$\frac{x}{x-2}$
=($\frac{x+2}{x-2}+\frac{4}{(x-2)^{2}}$)×$\frac{x-2}{x}$
=$\frac{x+2}{x}+\frac{4}{x(x-2)}$
=$\frac{(x+2)(x-2)+4}{x(x-2)}$
=$\frac{{x}^{2}}{x(x-2)}$
=$\frac{x}{x-2}$,
当x=1时,原式=$\frac{1}{1-2}=-1$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法,注意选取一个使得原分式有意义的值代入求值.

练习册系列答案
相关题目
2.在$-\frac{1}{7}$,-π,0,3.14,$-\sqrt{2}$,$\root{3}{-8}$,$-\sqrt{49}$,$\frac{{\sqrt{3}}}{2}$,76.012345678910111213…(小数部分由连续的正整数组成)中,无理数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
16. 四个图形是如图所示正方体的展开图的是( )
四个图形是如图所示正方体的展开图的是( )
 四个图形是如图所示正方体的展开图的是( )
四个图形是如图所示正方体的展开图的是( )| A. |  | B. |  | C. |  | D. |  |
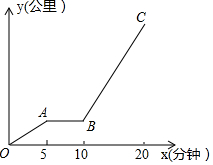 李狗蛋从家出发坐公交车去上学,他要先走到公交车站等公交车.他离家的距离y(米)与经过的时间x(分钟)的关系折线如图所示,已知狗蛋每分钟能走0.1公里,公交车的速度为0.4公里/分钟.
李狗蛋从家出发坐公交车去上学,他要先走到公交车站等公交车.他离家的距离y(米)与经过的时间x(分钟)的关系折线如图所示,已知狗蛋每分钟能走0.1公里,公交车的速度为0.4公里/分钟.
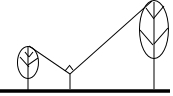 如图,身高1.5米的人站在两棵树之间,距较高的树5米,距较矮的树3米,若此人观察的树梢所成的视线的夹角是90°,且较矮的树高4米,那么较高的树有多少米?
如图,身高1.5米的人站在两棵树之间,距较高的树5米,距较矮的树3米,若此人观察的树梢所成的视线的夹角是90°,且较矮的树高4米,那么较高的树有多少米?