题目内容
19.(1)定义:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.如图1,四边形ABCD为凹四边形.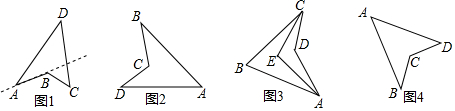
(2)性质探究:请完成凹四边形一个性质的证明.
已知:如图2,四边形ABCD是凹四边形.
求证:∠BCD=∠B+∠A+∠D.
(3)性质应用:
如图3,在凹四边形ABCD中,∠BAD的角平分线与∠BCD的角平分线交于点E,若∠ADC=140°,∠AEC=102°,则∠B=64°.
(4)类比学习:
如图4,在凹四边形ABCD中,点E,F,G,H分别是边AD,AB,BC,CD的中点,顺次连接各边中点得到四边形EFGH.若AB=AD,CB=CD,则四边形EFGH是C.(填写序号即可)
A.梯形 B.菱形 C.矩形 D.正方形.
分析 (2)延长BC交AD于点M,根据三角形的外角的性质即可解决问题.
(3)利用(2)中结论如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β,列出方程组即可解决问题.
(3)结论:四边形EFGH是矩形.利用三角形的中位线定理,首先证明是平行四边形,再证明有一个角是90度即可.
解答 解:(2)延长BC交AD于点M
∵∠BCD是△CDM的外角,
∴∠BCD=∠CMD+∠D,
同理∠CD是△ABM的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
(2)如图3中,设∠B=x,∠ECB=∠ECD=α,∠EAD=∠EAB=β.
由(2)可知,$\left\{\begin{array}{l}{140=102+α+β}\\{102=x+α+β}\end{array}\right.$,
解得x=64°
故答案为64.
(3)四边形EFGH是矩形,
证明:连接AC,BD,交EH于点M,
∵E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=HG=$\frac{1}{2}$AC,EF∥HG∥AC,
∴四边形EFGH是平行四边形,
∵AB=AD,BC=DC,
∴A、C在BD的垂直平分线上,
∴AM⊥EH,
已证EF∥AC,同理可证FG∥BD,
∴∠EFG=90°,
∴□EFGH是矩形;
故答案为C.
点评 本题考查了三角形的中位线性质,线段垂直平分线性质,平行四边形的判定,矩形的判定,三角形的外角性质的应用,能综合运用性质进行推理和画图是解此题的关键,综合性比较强,有一定的难度.

练习册系列答案
相关题目
7.计算(-a3)2的结果是( )
| A. | -a6 | B. | -a5 | C. | a6 | D. | a5 |
14.为测量底面为圆形的古塔的高度,以下是小明与小红的研究报告:
(1)写出小明的研究报告中“数据处理”的详细过程;
(2)指出小红研究报告中的错误之处;
(3)利用两人的测量数据,直接写出古塔底面圆的半径(结果精确到1m).
| 小明的研究报告 | 小红的研究报告 | |
| 测量图例 | 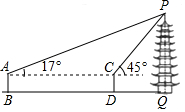 | 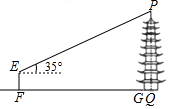 |
| 测量过程 | 如图,测角仪AB、CD的高度均为1.6m,分别测得古塔顶端的仰角为17°、45°,测角仪底端的距离(BD)为69m. | 如图,测角仪EF的高度为1.6m,测得古塔顶端的仰角为35°,测角仪所在位置与古塔底部边缘的最短距离(FG)为38.3m. |
| 参考数据 | sin17°≈0.29,cos17°≈0.96, tan17°≈0.31,$\sqrt{2}$≈1.41 | sin35°≈0.57,cos35°≈0.82, tan35°≈0.70 |
| 数据处理 | 32.6 | PQ=38.3×tan35°+1.6≈28.41(m) |
(2)指出小红研究报告中的错误之处;
(3)利用两人的测量数据,直接写出古塔底面圆的半径(结果精确到1m).
4.计算(-xy2)3的结果是( )
| A. | x3y6 | B. | -x3y6 | C. | -x4y5 | D. | x4y5 |
 已知:如图,∠C=∠EDB,∠2=∠3,求证:∠B=∠FDC.
已知:如图,∠C=∠EDB,∠2=∠3,求证:∠B=∠FDC.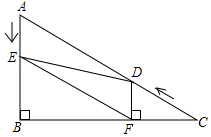 如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.