题目内容
14.为测量底面为圆形的古塔的高度,以下是小明与小红的研究报告:| 小明的研究报告 | 小红的研究报告 | |
| 测量图例 | 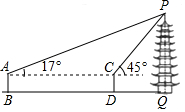 | 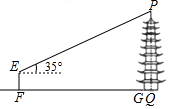 |
| 测量过程 | 如图,测角仪AB、CD的高度均为1.6m,分别测得古塔顶端的仰角为17°、45°,测角仪底端的距离(BD)为69m. | 如图,测角仪EF的高度为1.6m,测得古塔顶端的仰角为35°,测角仪所在位置与古塔底部边缘的最短距离(FG)为38.3m. |
| 参考数据 | sin17°≈0.29,cos17°≈0.96, tan17°≈0.31,$\sqrt{2}$≈1.41 | sin35°≈0.57,cos35°≈0.82, tan35°≈0.70 |
| 数据处理 | 32.6 | PQ=38.3×tan35°+1.6≈28.41(m) |
(2)指出小红研究报告中的错误之处;
(3)利用两人的测量数据,直接写出古塔底面圆的半径(结果精确到1m).
分析 (1)延长AC交PQ于点E.则AE⊥PQ,在直角△PCE和直角△PAE中利用PE表示出AE和CE的长,然后根据AC=AE-CE列方程求得PE的长,则PQ即可求得;
(2)根据解直角三角形和三角函数的定义判断;
(3)作EM⊥PQ于点M,在EM上取点C,使∠PCM=45°,求得FQ的长,根据半径GQ=FQ-FG求解.
解答  解:(1)延长AC交PQ于点E.则AE⊥PQ.(图1).
解:(1)延长AC交PQ于点E.则AE⊥PQ.(图1).
设PE=xm,
∵在Rt△PCE中,∠PCE=45°,
∴PE=CE=xm.
在Rt△APE中,tan∠PAE=$\frac{PE}{AE}$,
则AE=$\frac{PE}{tan∠PAE}$=$\frac{x}{tan15°}$=$\frac{x}{0.31}$,
又∵AE-CE=AC=BD,
∴$\frac{x}{0.31}$-x=69,
解得x=31,
则PQ=PE+EQ=PE+AB=31+1.6=32.6(m).
故答案是:32.6;
(2)错误的原因:PG与地面不垂直;
(3)作EM⊥PQ于点M,在EM上取点C,使∠PCM=45°,(图2)
则PM=CM=31(m),
在直角△PEM中,EM=$\frac{PM}{tan35°}$=$\frac{31}{tan35°}$=$\frac{31}{0.7}$≈44.3(m).
则FQ=EM=44.3(m).
∴GQ=44.4-38.3=6(m).
答:古塔底面圆的半径是6m.
点评 本题主要考查解直角三角形的应用,本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
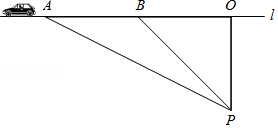 交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路1上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路1上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).
交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路1上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路1上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).