题目内容
14.阅读材料:材料 已知实数m、n满足m2-m-1=0、n2-n-1=0.且m≠n,求$\frac{n}{m}$+$\frac{m}{n}$的值.
解:由题知m、n是方程x2-x-1=0的两个不相等的实数根.根据材料1得m+n=1,mn=-1
∴$\frac{n}{m}$+$\frac{m}{n}$=$\frac{{m}^{2}+{n}^{2}}{mn}$=$\frac{(m+n)^{2}-2mn}{mn}$=$\frac{1+2}{-1}$=-3
根据上述材料解决下面问题:
(1)已知实数m、n满足3m2-3m-1=0、3n2-3n-1=0,且m≠n,求m2n+mn2的值.
(2)已知实数p、q满足p2=7p-2、2q2=7q-1,且p≠2q,求p2+4q2的值.
分析 (1)由实数m、n满足3m2-3m-1=0、3n2-3n-1=0,且m≠n,即可得出m、n是方程3x2-3x-1=0的两个不相等的实数根,根据根与系数的关系即可得出m+n=1、mn=-$\frac{1}{3}$,将代数式m2n+mn2提取公因式mn即可变形为mn(m+n),再代入m+n=1、mn=-$\frac{1}{3}$即可求出结论;
(2)由实数p、q满足p2=7p-2、2q2=7q-1,且p≠2q,即可得出p、2q是方程x2-7x+2=0的两个不相等的实数根,根据根与系数的关系即可得出p+2q=7、p•2q=2pq=2,利用配方法可将代数式p2+4q2变形为(p+2q)2-2×2pq,再代入p+2q=7、p•2q=2pq=2即可求出结论.
解答 解:(1)由题意知:m、n是方程3x2-3x-1=0的两个不相等的实数根,
∴m+n=1,mn=-$\frac{1}{3}$,
∴m2n+mn2=mn(m+n)=-$\frac{1}{3}$×1=-$\frac{1}{3}$.
(2)∵2q2=7q-1,
∴4q2-14q+2=0,即(2q)2-7×2q+2=0.
又∵p2=7p-2,即p2-7p+2=0,
∴p、2q是方程x2-7x+2=0的两个不相等的实数根,
∴p+2q=7,p•2q=2pq=2,
∴p2+4q2=(p+2q)2-2×2pq=72-2×2=45.
点评 本题考查了根与系数的关系,解题的关键是:(1)根据根与系数的关系找出m+n=1、mn=-$\frac{1}{3}$;(2)根据根与系数的关系找出p+2q=7、p•2q=2pq=2.

练习册系列答案
相关题目
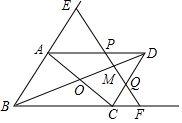 如图,已知?ABCD的对角线交于O点,M为OD的中点,过M的直线分别交AD、CD于P、Q.交BA、BC的延长线于E、F.求证:PE+QF=2PQ.
如图,已知?ABCD的对角线交于O点,M为OD的中点,过M的直线分别交AD、CD于P、Q.交BA、BC的延长线于E、F.求证:PE+QF=2PQ.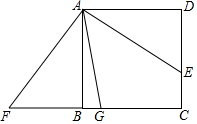 如图,E是正方形ABCD上一点,△ABF由△ADE旋转所得
如图,E是正方形ABCD上一点,△ABF由△ADE旋转所得