化简:$\frac{2x}{{x}^{2}-1}$÷•÷$\frac{x-2}{x-1}$•$\frac{x-1}{x-2}$．题目和参考答案——青夏教育精英家教网—

题目内容

6．化简：$\frac{2x}{{x}^{2}-1}$÷（1-$\frac{1}{x+1}$）•（1+$\frac{1}{1-x}$）÷$\frac{x-2}{x-1}$•$\frac{x-1}{x-2}$．

分析根据分式的混合运算法则计算即可．

解答解：原式=$\frac{2x}{{x}^{2}-1}$÷$\frac{x}{x+1}$•$\frac{2-x}{1-x}$÷$\frac{x-2}{x-1}$•$\frac{x-1}{x-2}$
=$\frac{2x}{（x+1）（x-1）}$×$\frac{x+1}{x}$×$\frac{2-x}{1-x}$×$\frac{x-1}{x-2}$×$\frac{x-1}{x-2}$
=$\frac{2}{x-2}$．

点评本题考查的是分式的混合运算，掌握分式的混合运算法则、因式分解是解题的关键．

练习册系列答案

天下无题系列丛书绿色假期寒假作业系列答案

中学生学习报寒假专刊系列答案

创新成功学习快乐寒假云南科技出版社系列答案

快乐假期寒假作业内蒙古人民出版社系列答案

17．先让我们一起来学习方程m²+1=$\sqrt{{m}^{2}+3}$的解法：
解：令m²=a，则a+1=$\sqrt{a+3}$，方程两边平方可得，（a+1）²=a+3
解得a₁=1，a₂=-2，∵m²≥0∴m²=1∴m=±1
点评：类似的方程可以用“整体换元”的思想解决．
不妨一试：
如图1，在平面直角坐标系xOy中，抛物线y=ax²+1经过点A（4，-3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．

（1）求抛物线的解析式；
（2）①当P点运动到A点处时，通过计算发现：PO=PH（填“＞”、“＜”或“=”）；
②当P点在抛物线上运动时，猜想PO与PH有何数量关系，并证明你的猜想；
（3）当△PHO为等边三角形时，求点P坐标；
（4）如图2，设点C（1，-2），问是否存在点P，使得以P、O、H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．

14．阅读材料：
材料已知实数m、n满足m²-m-1=0、n²-n-1=0．且m≠n，求$\frac{n}{m}$+$\frac{m}{n}$的值．
解：由题知m、n是方程x²-x-1=0的两个不相等的实数根．根据材料1得m+n=1，mn=-1
∴$\frac{n}{m}$+$\frac{m}{n}$=$\frac{{m}^{2}+{n}^{2}}{mn}$=$\frac{（m+n）^{2}-2mn}{mn}$=$\frac{1+2}{-1}$=-3
根据上述材料解决下面问题：
（1）已知实数m、n满足3m²-3m-1=0、3n²-3n-1=0，且m≠n，求m²n+mn²的值．
（2）已知实数p、q满足p²=7p-2、2q²=7q-1，且p≠2q，求p²+4q²的值．

1．

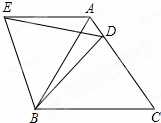在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED．
（1）求证：AE∥BC；
（2）若BC=5，BD=4，求△ADE的周长．

11．解方程：
（1）x²-6x+8=0
（2）（x-5）²=2（x-5）-1．

18．已知9+$\sqrt{13}$的小数部分是a，9-$\sqrt{13}$的整数部分是b，求ab-3a+4b+8的值．

15．已知$\frac{b+c}{a}$=$\frac{a+c}{b}$=$\frac{a+b}{c}$=m．求m的值．

试题分类