题目内容
18.先化简,再求值:(1-$\frac{x}{{x}^{2}+x}$)÷$\frac{{x}^{2}-1}{{x}^{2}+2x+1}$,其中x=2.分析 先算括号里面的,再算除法,把x=2代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}}{x(x+1)}$•$\frac{x+1}{x-1}$
=$\frac{x}{x+1}$•$\frac{x+1}{x-1}$
=$\frac{x}{x-1}$,
当x=2时,原式=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在Rt△ABC中,∠C=90°,BC=6,AC=8,则cos∠BAC等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
3.下列命题错误的是( )
| A. | 矩形的对角线相等 | |
| B. | 平行四边形的对角线互相平分 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
7.某玩具店试销售一种进价为20元的新型玩具,根据物价部门规定:该玩具售价不得超过90元.在连续七天的试销售过程中,玩具店就销售量y(个)与售价x(元)之间的变化关系做了如表记录.
(1)运用所学过的函数知识,试判断y与x之间的函数关系,并求y与x的函数关系式;
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 售价x | 30 | 30 | 35 | 40 | 40 | 40 | 45 |
| 销售量y | 100 | 100 | 95 | 90 | 90 | 90 | 85 |
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
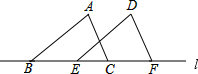 已知△ABC的边在直线l上,BC=5,现把△ABC沿着直线l向右平移到△DEF的位置(如图所示),若EC=3,则△ABC平移的距离为( )
已知△ABC的边在直线l上,BC=5,现把△ABC沿着直线l向右平移到△DEF的位置(如图所示),若EC=3,则△ABC平移的距离为( ) 如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).
如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).