题目内容
6. 如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).
如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).(1)请在方格中建立直角坐标系,并写出C点的坐标(2,1).
(2)请画出△ABC向下平移1个单位,再向右平移2个单位后的△A′B′C′.若△ABC内部存在一点M(a,b),则它在△A′B′C′内的对应点M′的坐标是(a+2,b-1).
(3)求△ABC的面积.
分析 (1)以点A向左一个单位,向下4个单位为坐标原点建立平面直角坐标系,然后写出点C的坐标即可;
(2)根据平面直角坐标系找出点A′、B′、C′的位置,然后顺次连接即可,再根据平移规律写出点M′的坐标;
(3)用△ABC所在的矩形的面积减去四周三个直角三角形的面积,列式计算即可得解.
解答 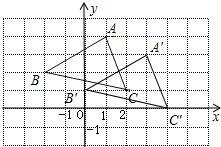 解:(1)建立平面直角坐标系如图,C(2,1);
解:(1)建立平面直角坐标系如图,C(2,1);
(2)△A′B′C′如图所示,M′(a+2,b-1);
(3)△ABC的面积S=3×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×3,
=12-3-2-1.5,
=5.5.
故答案为:(2,1);(a+2,b-1).
点评 本题考查了利用平移变换作图,平面直角坐标系的定义,准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
16.-2,0,0.5,-$\sqrt{2}$这四个数中,属于无理数的是( )
| A. | -2 | B. | 0 | C. | 0.5 | D. | -$\sqrt{2}$ |
1.观察下列各数:1,1,$\frac{5}{7}$,$\frac{7}{15}$,$\frac{9}{31}$,…按你发现的规律计算这列数的第7个数为( )
| A. | $\frac{15}{255}$ | B. | $\frac{13}{127}$ | C. | $\frac{11}{127}$ | D. | $\frac{11}{63}$ |
15.已知一个三角形的两边长分别是2和7,第三边为偶数,则此三角形的周长是( )
| A. | 15 | B. | 16 | C. | 17 | D. | 15或17 |
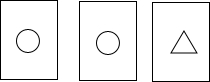 小宇手中有15张牌,其中10张牌的背面标记“〇”,5张牌的背面标记“△”,如图是从小宇手中取出的3张牌.若从手中剩余的牌中随机抽出一张牌,每张牌被抽出的机会相等,则抽出标记“○”的牌的概率是$\frac{2}{3}$.
小宇手中有15张牌,其中10张牌的背面标记“〇”,5张牌的背面标记“△”,如图是从小宇手中取出的3张牌.若从手中剩余的牌中随机抽出一张牌,每张牌被抽出的机会相等,则抽出标记“○”的牌的概率是$\frac{2}{3}$.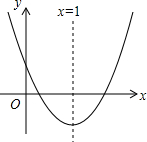 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )