题目内容
8.如图,三角形有一边上的中线长恰好等于这边的长,那么这个三角形可称为“等中三角形”,探索体验
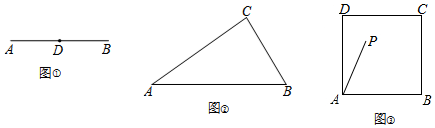
(1)如图①,点D是线段AB的中点,请画一个△ABC,使其为“等中三角形”.
(2)如图②,在 Rt△ABC中,∠C=90°,AC=2,BC=$\sqrt{3}$,判断△ABC是否为“等中三角形”,并说明理由.
拓展应用
(3)如图③,正方形ABCD木板的边长AB=6,请探索在正方形木板上是否存在点P,使△ABP为面积最大的“等中三角形”?若存在,求出CP的长;若不存在,请说明理由.
分析 (1)通过同圆的半径相等,取DC=AB,则△ABC就是所求作的等中三角形;
(2)作中线BD,根据勾股定理求中线BD=AC,则△ABC是“等中三角形”;
(3)分别以△ABP三边画等中三角形,对比后得图5中的等中三角形的面积最大,求出此时的CP的长即可.
解答 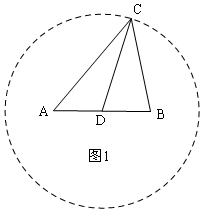 解:(1)如图1,
解:(1)如图1,
作法:①以D为圆心,以AB为半径画圆,在圆上任意取一点C,
②连接AC、BC,
则△ABC就是所求作的“等中三角形”;
(2)△ABC是“等中三角形”,理由是:
如图2,取AC的中点D,连接BD,
∵AC=2,
∴CD=$\frac{1}{2}$AC=1,
∵∠ACB=90°,
由勾股定理得:BD=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴BD=AC,
∴△ABC是“等中三角形”,
(3)分三种情况:
①当中线长BE=AP时,如图3,
画法:①在正方形内任意取一点P,连接AP,取中点E,
②以E为圆心,以AP为半径画圆,当圆E经过点B时,△ABP是等中三角形;


②当中线长AE=PB时,同理可画出图4;
③当中线长PE=AB时,如图5,
画法:取AB中点E,以E为圆心,以AB为半径画圆,交CD于P,此时,△ABP是等中三角形;
由三个图形可得:图5中的等中三角形的面积最大,
此时,P是DC的中点,
∴PC=$\frac{1}{2}$CD=$\frac{1}{2}×6$=3.
点评 本题是四边形的综合题,考查了正方形的性质、直角三角形斜边中线的性质,等腰三角形的性质以及三角形全等的性质和判定,又是一道新定义的阅读理解问题及尺规作图题,综合性较强;熟练掌握性质和定理是关键,并注意理解和运用已知的“中线长恰好等于这边的长”这一条件.

练习册系列答案
相关题目
19.对于任意实数x,点P(x,x2+4x+3)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
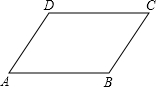 如图,AD∥BC,∠BAD=∠BCD,求证:AB∥CD.
如图,AD∥BC,∠BAD=∠BCD,求证:AB∥CD.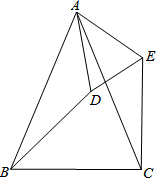 如图,△ABC和△ADE都是顶角为45°的等腰三角形,BC、DE分别是这两个等腰三角形的底边.图中的△ACE可以看成由哪个三角形通过怎样的旋转得到的?证明△ACE与这三角形全等.
如图,△ABC和△ADE都是顶角为45°的等腰三角形,BC、DE分别是这两个等腰三角形的底边.图中的△ACE可以看成由哪个三角形通过怎样的旋转得到的?证明△ACE与这三角形全等. 已知:如图,AC⊥BC,DE⊥BC,求证:∠BDE=∠A.
已知:如图,AC⊥BC,DE⊥BC,求证:∠BDE=∠A. 按要求完成下列问题:
按要求完成下列问题: