题目内容
20.在△ABC中,∠C=90°,sinA=$\frac{1}{4}$,则tanB=$\sqrt{15}$.分析 根据同角三角函数关系,可得cotA,根据一个角的正切等于它余角的余切,可得答案.
解答 解:cosA=$\sqrt{1-(\frac{1}{4})^{2}}$=$\frac{\sqrt{15}}{4}$,
cotA=$\frac{cosa}{sinA}$=$\sqrt{15}$,
△ABC中,∠C=90°,sinA=$\frac{1}{4}$,
tanB=cotA=$\frac{cosa}{sinA}$=$\sqrt{15}$,
故答案为:$\sqrt{15}$.
点评 本题考查了互余两角三角函数关系,同角三角函数关系,可得cotA,根据一个角的正切等于它余角的余切.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.关于二次函数y=x2-2x-3的图象,下列说法中错误的是( )
| A. | 当x<2,y随x的增大而减小 | B. | 函数的对称轴是直线x=1 | ||
| C. | 函数的开口方向向上 | D. | 函数图象与y轴的交点坐标是(0,-3) |
12.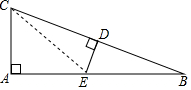 如图,在 Rt△ABC 中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )
如图,在 Rt△ABC 中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )
 如图,在 Rt△ABC 中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )
如图,在 Rt△ABC 中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )| A. | 4cm | B. | 8cm | C. | 16cm | D. | 32cm |
9. 如图,已知AB∥CD,下列各角之间的关系一定成立的是( )
如图,已知AB∥CD,下列各角之间的关系一定成立的是( )
 如图,已知AB∥CD,下列各角之间的关系一定成立的是( )
如图,已知AB∥CD,下列各角之间的关系一定成立的是( )| A. | ∠1=∠3 | B. | ∠2=∠4 | C. | ∠1>∠4 | D. | ∠3+∠5=180° |
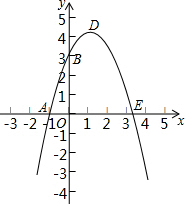 已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.