题目内容
15.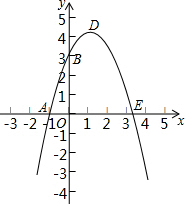 已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出P点的坐标,若不存在说明理由.
分析 (1)把A点和B点坐标分别代入y=-x2+bx+c得到关于b、c的方程组,然后解方程组即可;
(2)通过解方程-x2+2x+3=0得到E点坐标,再把一般式配成顶点式得到D点坐标,然后根据三角形面积公式计算△ODE的面积;连接BE交直线x=1于点P,如图,利用两点之间线段最短可判断此时PA+PB的值最小,然后求出BE的解析式后易得P点坐标.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{-1-b+c=0}\\{c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=-x2+2x+3;
(2)当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,则E(3,0);
y=-(x-1)2+4,则D(1,4),
∴S△ODE=$\frac{1}{2}$×3×4=6;
连接BE交直线x=1于点P,如图,则PA=PE,
∴PA+PB=PE+PB=BE,
此时PA+PB的值最小,
易得直线BE的解析式为 y=-x+3.,
当x=1时,y=-x+3=3,
∴P(1,2).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了最短路径问题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
5.三角形三条边大小之间存在一定的关系,以下列各组线段为边,能组成三角形的是( )
| A. | 2cm、3cm、5cm | B. | 5cm、6cm、10cm | C. | 1cm、1cm、3cm | D. | 3cm、4cm、9cm |
6.一条直线上有8个点,则以这8个点为端点的线段共有( )
| A. | 7条 | B. | 14条 | C. | 16条 | D. | 28条 |
3.某商场对上周某品牌运动鞋的销售情况进行了统计,如表所示:
经理决定本周进货时多进一些23.5cm尺码的运动鞋,可用来解释这一决定的统计知识是( )
| 尺码 | 22 | 22.5 | 23 | 23.5 | 24 |
| 销售量/双 | 1 | 2 | 5 | 11 | 7 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 平均数与中位数 |
10.下列各组中的两项不属于同类项的是( )
| A. | 3m2n3和-m2n3 | B. | a3和x3 | C. | -1 和π | D. | $\frac{xy}{5}$和25yx |
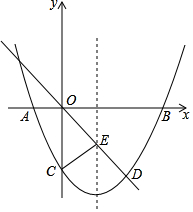 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).