题目内容
12.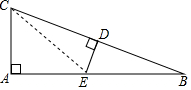 如图,在 Rt△ABC 中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )
如图,在 Rt△ABC 中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )| A. | 4cm | B. | 8cm | C. | 16cm | D. | 32cm |
分析 连接CE,先由三角形内角和定理求出∠B的度数,再由线段垂直平分线的性质及三角形内角和定理求出∠ACE及∠CEA的度数,由直角三角形中30°的角所对的直角边是斜边的一半即可解答.
解答 解:连接CE,
∵Rt△ABC中,∠A=90°,∠BCA=75°,
∴∠B=90°-∠BCA=90°-75°=15°,
∵DE垂直平分BC,
∴∠BCE=∠B=15°,BE=CE,
∴∠ACE=∠BCA-∠BCE=75°-15°=60°,
∵Rt△AEC中,∠ACE=∠BCA=60°,AC=8cm,
∴∠AEC=90°-∠ACE=90°-60°=30°,
∴CE=2AC=16cm,
∵BE=CE,
∴BE=16cm.
故选C.
点评 本题考查的是直角三角形及线段垂直平分线的性质,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
2.下列运算正确的是( )
| A. | a8÷a2=a4 | B. | a5-(-a)2=a3 | C. | a3•(-a)2=a5 | D. | 5a+3b=8ab |
3.某商场对上周某品牌运动鞋的销售情况进行了统计,如表所示:
经理决定本周进货时多进一些23.5cm尺码的运动鞋,可用来解释这一决定的统计知识是( )
| 尺码 | 22 | 22.5 | 23 | 23.5 | 24 |
| 销售量/双 | 1 | 2 | 5 | 11 | 7 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 平均数与中位数 |
1.已知|x|=3,y2=4,且x+y<0,则x-y的值等于( )
| A. | -5 | B. | -1 | C. | ±5 | D. | -5或-1 |
2.王涛从家走到汽车站,第一小时走了3km,他看了看表,估计按这个速度将迟到40min,因此,他以每小时4km的速度走剩余的路,结果反而提前了45min到达,求王涛家到汽车站的距离,如果设王涛家到汽车站的距离为xkm,则可列方程为( )
| A. | $\frac{x}{3}$+$\frac{2}{3}$=$\frac{x}{4}$-$\frac{3}{4}$ | B. | $\frac{x}{3}$-$\frac{2}{3}$=$\frac{x}{4}$+$\frac{3}{4}$ | C. | $\frac{x}{3}$+$\frac{2}{3}$=$\frac{x-3}{4}$-$\frac{7}{4}$ | D. | $\frac{x}{3}$-$\frac{2}{3}$=$\frac{x-3}{4}$+$\frac{7}{4}$ |
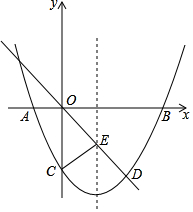 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).