题目内容
4.已知方程x2-mx+6=0的一个根为2,则m=5,另一个根为3.分析 根据一元二次方程的解的定义,将x=2代入关于x的方程x2-mx+6=0,然后解关于m的一元一次方程;再根据根与系数的关系x1+x2=-$\frac{b}{a}$解出方程的另一个根.
解答 解:根据题意,得
4-2m+6=0,
解得,m=5;
由韦达定理,知
x1+x2=m;
即2+x2=5,
解得,x2=3.
故答案是:5,3.
点评 本题主要考查了一元二次方程的解的定义、根与系数的关系.在利用根与系数的关系x1+x2=-$\frac{b}{a}$、x1•x2=$\frac{c}{a}$来计算时,要弄清楚a、b、c的意义.

练习册系列答案
相关题目
14.(-0.7)2的平方根是( )
| A. | 0.49 | B. | -0.7 | C. | 0.7 | D. | ±0.7 |
19.已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$,则$\frac{x+3y-z}{2x-y+z}$的值是( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{2}$ |
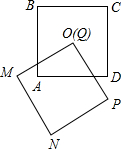 如图是两个全等的正方形,把正方形QMNP的一个顶点Q放置在正方形ABCD的中心O处,绕点O旋转正方形QMNP,求证:两个正方形公共部分的面积为定值.
如图是两个全等的正方形,把正方形QMNP的一个顶点Q放置在正方形ABCD的中心O处,绕点O旋转正方形QMNP,求证:两个正方形公共部分的面积为定值.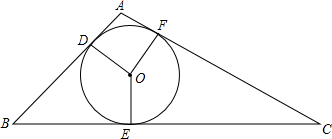 如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.