题目内容
19．已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$，则$\frac{x+3y-z}{2x-y+z}$的值是（ ）| A． | 1 | B． | $\frac{3}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{3}{2}$ |
分析 根据比例性质，可用x表示y，用x表示z，根据分式的性质，可得答案．
解答 解：由$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$，得
y=$\frac{3x}{2}$，z=$\frac{5x}{2}$．
$\frac{x+3y-z}{2x-y+z}$=$\frac{x+3×\frac{3x}{2}-\frac{5x}{2}}{2x-\frac{3x}{2}+\frac{5x}{2}}$=$\frac{3x}{3x}$=1．
故选：A．
点评 本题考查了比例的性质，利用比例的性质得出y=$\frac{3x}{2}$，z=$\frac{5x}{2}$是解题关键，又利用了分式的性质．
练习册系列答案
相关题目
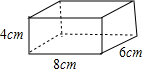如图所示的是一个长8cm，宽6cm，高4cm的长方体，现在把它等分为24个棱长为2cm的小正方体
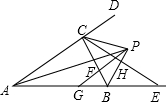如图，∠BAC与∠CBE的平分线相交于点P，BE=BC，PB与CE交于点H，PG∥AD交BC于F，交AB于G，下列结论：
14．已知等腰三角形的一边长是9cm，另一边长是5cm，那么这个等腰三角形的周长是（ ）
| A． | 19cm | B． | 23cm | C． | 16cm | D． | 19cm或23cm |
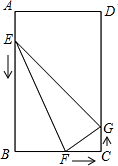如图，在矩形ABCD中，AB=12cm，BC=8cm，点E、F、G分别从点A、B、C三点同时出发，沿矩形的边按逆时针方向移动，点E，G的速度均为2cm/s，点F的速度为4cm/s，当点F追上点G（即点F与点G重合）时，三个点随之停止移动．设移动开始后第t秒时，△EFG的面积为S（cm2）．