题目内容
8.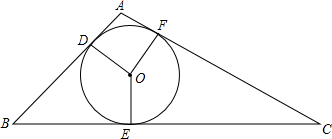 如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
如图所示,⊙O是△ABC的内切圆,D、E、F为切点,若$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,求△ABC的最大内角的度数.
分析 首先求得弧DF的度数,从而可得到∠DOF的度数,然后由切线的性质可知∠ODA=∠OFA=90°,从而可求得∠A的度数.
解答 解:∵$\widehat{DF}$,$\widehat{DE}$,$\widehat{EF}$的度数之比为5:9:10,
∴$\widehat{DF}$的度数=360°×$\frac{5}{24}$=75°,
∵⊙O是△ABC的内切圆,D、E、F为切点,
∴∠ODA=∠OFA=90°.
∴∠A+∠DOF=180°.
∴∠A=180°-75°=105°.
∴△ABC的最大内角的度数为105°.
点评 本题主要考查的是三角形的内切圆和内心,求得∠A+∠DOF=180°是解题的关键.

练习册系列答案
相关题目
17.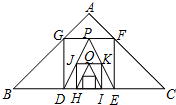 如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )
 如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )| A. | $\frac{2}{3}•{(\frac{1}{2})^{n-1}}$ | B. | $\frac{{2\sqrt{2}}}{3}•{(\frac{1}{2})^{n-1}}$ | C. | $\frac{2}{3}•{(\frac{1}{2})^n}$ | D. | $\frac{{2\sqrt{2}}}{3}•{(\frac{1}{2})^n}$ |
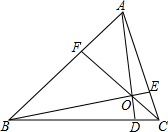 如图.已知△ABC,点E在AC上,点F在AB上,BE与CF交于点O,AD过点O交BC于点D,且AF:BF=1:2.CE:AC=1:4.求BD:DC的值.
如图.已知△ABC,点E在AC上,点F在AB上,BE与CF交于点O,AD过点O交BC于点D,且AF:BF=1:2.CE:AC=1:4.求BD:DC的值.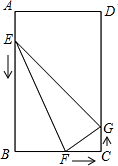 如图,在矩形ABCD中,AB=12cm,BC=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).
如图,在矩形ABCD中,AB=12cm,BC=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).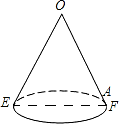 如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.
如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.