题目内容
13.将抛物线y=x2向下平移2个单位后,所得到的抛物线与直线y=x交于A,B两点,且平移后的抛物线的顶点为C,试求△ABC的面积.分析 根据平移的规律“左加右减,上加下减”求得平移后抛物线的解析式,则易求点A、B、C的坐标,所以根据三角形的面积公式进行解答即可.
解答 解:抛物线y=x2向下平移2个单位后抛物线的解析式为:y=x2-2.
所以新抛物线的顶点C的坐标是(0,-2).
由$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}-2}\end{array}\right.$得到:$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$,
则A(2,2),B(-1,-1),
∴△ABC的面积=$\frac{1}{2}$OC•(|xA|+|xB|)=$\frac{1}{2}$×2×3=3.
点评 本题考查二次函数图象与几何变换.也可以用平移规律“左加右减,上加下减”直接代入函数解析式求得平移后的函数解析式.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.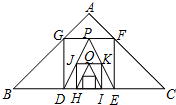 如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )
 如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )| A. | $\frac{2}{3}•{(\frac{1}{2})^{n-1}}$ | B. | $\frac{{2\sqrt{2}}}{3}•{(\frac{1}{2})^{n-1}}$ | C. | $\frac{2}{3}•{(\frac{1}{2})^n}$ | D. | $\frac{{2\sqrt{2}}}{3}•{(\frac{1}{2})^n}$ |
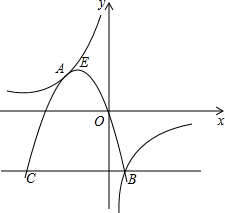 如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E. 如图,$\widehat{AB}$与弦AB哪条长?为什么?
如图,$\widehat{AB}$与弦AB哪条长?为什么?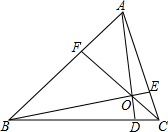 如图.已知△ABC,点E在AC上,点F在AB上,BE与CF交于点O,AD过点O交BC于点D,且AF:BF=1:2.CE:AC=1:4.求BD:DC的值.
如图.已知△ABC,点E在AC上,点F在AB上,BE与CF交于点O,AD过点O交BC于点D,且AF:BF=1:2.CE:AC=1:4.求BD:DC的值.