题目内容
11.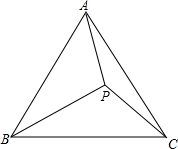 如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求:
如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求:(1)∠APC的度数;
(2)求△ABC的边长.
分析 (1)先把△APC绕点A顺时针旋转60°可得到△ABD,如图,根据旋转的性质得AD=AP=3,BD=PC=4,∠DAP=60°,∠ADB=∠APC,则可判断△ADP为等边三角形,所以DP=AP=3,∠ADP=60°,然后利用勾股定理的逆定理证明△BDP为直角三角形,∠BDP=90°,于是得到∠ADB=∠ADP+∠BDP=150°,
(2)作BE⊥AD于E,如图,先计算∠BDE=30°,再利用含30度的直角三角形三边的关系得到BE=$\frac{1}{2}$BD=2,DE=$\sqrt{3}$BE=2$\sqrt{3}$,然后在Rt△ABE中利用勾股定理计算AB.
解答 解:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
把△APC绕点A顺时针旋转60°可得到△ABD,如图,
∴AD=AP=3,BD=PC=4,∠DAP=60°,∠ADB=∠APC,
∴△ADP为等边三角形,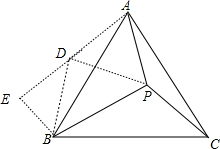
∴DP=AP=3,∠ADP=60°,
在△BDP中,∵DP=3,DB=4,BP=5,
而32+42=52,
∴DP2+DB2=BP2,
∴△BDP为直角三角形,∠BDP=90°,
∴∠ADB=∠ADP+∠BDP=60°+90°=150°,
∴∠APC=150°;
(2)作BE⊥AD于E,如图,
∵∠ADB=150°,
∴∠BDE=30°,
在Rt△BDE中,BE=$\frac{1}{2}$BD=2,DE=$\sqrt{3}$BE=2$\sqrt{3}$,
∴AE=AD+DE=3+2$\sqrt{3}$,
在Rt△ABE中,AB=$\sqrt{B{E}^{2}+A{E}^{2}}$=$\sqrt{{2}^{2}+(3+2\sqrt{3})^{2}}$=$\sqrt{25+12\sqrt{3}}$,
即△ABC的边长为$\sqrt{25+12\sqrt{3}}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质和勾股定理的逆定理.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 在△ABC中,AB=15,AC=20,∠B-∠C=90°,则线段BC的长度为7.
在△ABC中,AB=15,AC=20,∠B-∠C=90°,则线段BC的长度为7.
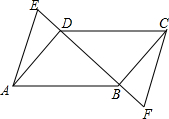 已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.
已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.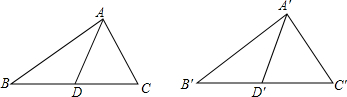
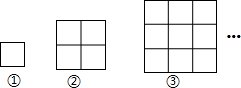 如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图象含有正方形的个数是( )
如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图象含有正方形的个数是( )