题目内容
16. 在△ABC中,AB=15,AC=20,∠B-∠C=90°,则线段BC的长度为7.
在△ABC中,AB=15,AC=20,∠B-∠C=90°,则线段BC的长度为7.
分析 作AD⊥CB交CB的延长线于D,先证明△ABD∽△CAD,得到AD、CD的关系,设CD=4x,由勾股定理表示出AC,求出x,再由勾股定理求出BD,即可得出结果.
解答 解:作AD⊥CB交CB的延长线于D,如图所示:
∵∠ABC-∠ACB=90°,又∠ABC-∠BAD=90°,
∴∠BAD=∠ACB,又∠D=∠D=90°,
∴△ABD∽△CAD,
∴$\frac{AB}{AC}$=$\frac{AD}{CD}$=$\frac{15}{20}$=$\frac{3}{4}$,
设CD=4x,则AD=3x,
由勾股定理得,AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{9{x}^{2}+16{x}^{2}}$=5x,
∴5x=20,
则x=4,
∴CD=16,AD=12,
由勾股定理得,BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{5}^{2}-1{2}^{2}}$=9,
∴BC=BD-CD=16-9=7,
故答案为7.
点评 本题考查了相似三角形的判定和性质、勾股定理等知识;正确作出辅助线、灵活运用勾股定理是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.为了解长城小区“全民健身”活动的开展情况,随机对该小区的40名居民一周的体育锻炼时间进行了统计,结果如表:
这40名居民一周体育锻炼时间的中位数是5小时.
| 锻炼时间(时) | 3 | 4 | 5 | 6 | 7 |
| 人数(人) | 6 | 13 | 14 | 5 | 2 |
8.在平面直角坐标系中,抛物线C1:y=$\frac{1}{2}$x2经过平移得到C2:y=$\frac{1}{2}$x2-2x,则C1平移得到C2的说法正确的是( )
| A. | 向左平移2个单位长度 | |
| B. | 向右平移2个单位长度 | |
| C. | 先向左平移2个单位长度,再向下平移2个单位长度 | |
| D. | 先向右平移2个单位长度,再向下平移2个单位长度 |
9.二次函数$y=-\frac{1}{2}{({x+3})^2}-2$的顶点坐标是( )
| A. | (3,2) | B. | (3,-2) | C. | (-3,-2) | D. | (-3,2) |
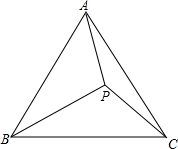 如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求:
如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求: