题目内容
20.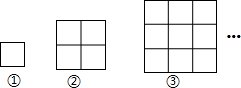 如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图象含有正方形的个数是( )
如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图象含有正方形的个数是( )| A. | 102 | B. | 91 | C. | 55 | D. | 31 |
分析 根据图形的变化规律可以得知每个图形比前一个图形多它序号的平方数个正方形,从而得出结论.
解答 解:结合图形可知,第②个图形比第①分图形多22个正方形,第③个比第②个多32个正方形,…,
即多的个数为序号的平方数,
∴第⑥个图象含有正方形的个数是1+22+32+42+52+62=91.
故选B.
点评 本题考查了图形的变化,解题的关键是发现“每个图形比前一个图形多它序号的平方数个正方形”.本题难度中等,如果一个个画出来去数,太耽误时间,这就需要在图形中寻找规律,解决此类型的题目就需要学生有良好的数列常识,能够及时发现变化规律才能快速的解决问题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
8.在平面直角坐标系中,抛物线C1:y=$\frac{1}{2}$x2经过平移得到C2:y=$\frac{1}{2}$x2-2x,则C1平移得到C2的说法正确的是( )
| A. | 向左平移2个单位长度 | |
| B. | 向右平移2个单位长度 | |
| C. | 先向左平移2个单位长度,再向下平移2个单位长度 | |
| D. | 先向右平移2个单位长度,再向下平移2个单位长度 |
15.下列方程变形不正确的是( )
| A. | -2x-3=5变形为-2x=5+3 | B. | 2(x-1)=-4变形为2x-2=-4 | ||
| C. | $\frac{x}{2}$+1=$\frac{x-1}{3}$变形为 3x+6=2(x-1) | D. | -2x=6变形为x=-$\frac{1}{3}$ |
9.二次函数$y=-\frac{1}{2}{({x+3})^2}-2$的顶点坐标是( )
| A. | (3,2) | B. | (3,-2) | C. | (-3,-2) | D. | (-3,2) |
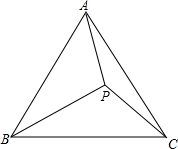 如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求:
如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求: 在直角梯形ABCD中,AD∥BC,∠DAB=90°,AD=1,BC=2.连接BD,把△ABD绕着点B逆时针旋转90°得到△EBF,若点F刚好落在DA的延长线上,则∠C=45°.
在直角梯形ABCD中,AD∥BC,∠DAB=90°,AD=1,BC=2.连接BD,把△ABD绕着点B逆时针旋转90°得到△EBF,若点F刚好落在DA的延长线上,则∠C=45°.