题目内容
16.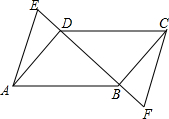 已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.
已知,如图,E,D,B,F在同一条直线上,AD∥CB,∠BAD=∠BCD,DE=BF,求证:AE∥CF.
分析 利用全等三角形的判定方法得出△ADB≌△CBD(AAS),进而证明△ADE≌△CBF(SAS),再利用平行线的判定方法得出答案.
解答 证明:∵AD∥CB,
∴∠ADB=∠CBD,可得:∠ADE=∠CBF,
在△ADB和△CBD中
∵$\left\{\begin{array}{l}{∠BAD=∠BCD}\\{∠ADB=∠CBD}\\{BD=BD}\end{array}\right.$,
∴△ADB≌△CBD(AAS),
∴AD=BC,
在△ADE和△CBF中
∵$\left\{\begin{array}{l}{DE=BF}\\{∠ADE=∠CBF}\\{AD=BC}\end{array}\right.$,
∴△ADE≌△CBF(SAS),
∴∠E=∠F,
∴AE∥CF.
点评 此题主要考查了全等三角形的判定与性质以及平行线的判定,正确得出△ADB≌△CBD是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
8.在平面直角坐标系中,抛物线C1:y=$\frac{1}{2}$x2经过平移得到C2:y=$\frac{1}{2}$x2-2x,则C1平移得到C2的说法正确的是( )
| A. | 向左平移2个单位长度 | |
| B. | 向右平移2个单位长度 | |
| C. | 先向左平移2个单位长度,再向下平移2个单位长度 | |
| D. | 先向右平移2个单位长度,再向下平移2个单位长度 |
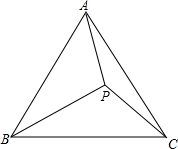 如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求:
如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求: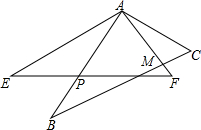 如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠BAE=24°,∠F=57°,边BC与AF相交于点M,边AB与EF相交于点P.
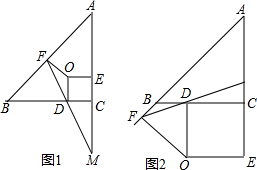
如图,在△ABC和△AEF中,∠B=∠E,AB=AE,BC=EF,∠BAE=24°,∠F=57°,边BC与AF相交于点M,边AB与EF相交于点P. 在直角梯形ABCD中,AD∥BC,∠DAB=90°,AD=1,BC=2.连接BD,把△ABD绕着点B逆时针旋转90°得到△EBF,若点F刚好落在DA的延长线上,则∠C=45°.
在直角梯形ABCD中,AD∥BC,∠DAB=90°,AD=1,BC=2.连接BD,把△ABD绕着点B逆时针旋转90°得到△EBF,若点F刚好落在DA的延长线上,则∠C=45°.