题目内容
1.已知关于x的一元二次方程x2-kx+k-1=0.(1)求证:此一元二次方程恒有实数根.
(2)无论k为何值,该方程有一根为定值,请求出此方程的定值根.
分析 (1)由根的判别式的符号来判定关于x的一元二次方程x2-kx+k-1=0的根的情况.
(2)利用求根根式求得方程的两个根,得到其中一根是常数.
解答 (1)证明:∵△=b2-4ac=(-k)2-4×1×(k-1)=k2-4k+4=(k-2)2≥0,
∴此一元二次方程恒有实数根.
(2)解:解方程x2-kx+k-1=0,得
$x=\frac{{-(-k)±\sqrt{{{(k-2)}^2}}}}{2×1}=\frac{k±(k-2)}{2}$,
解得x1=k-1,x2=1.
其中根X=1与k的取值无关,所以此方程的定值根为x=1.
点评 本题考查了根的判别式,一元二次方程的解的定义.
总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
9.二次函数$y=-\frac{1}{2}{({x+3})^2}-2$的顶点坐标是( )
| A. | (3,2) | B. | (3,-2) | C. | (-3,-2) | D. | (-3,2) |
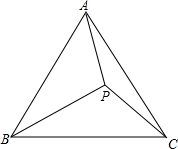 如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求:
如图,已知P是等边△ABC内一点,PA=3,PC=4,PB=5.求: