题目内容
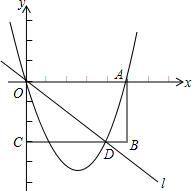 已知矩形OABC在平面直角坐标系中位置如图所示,A点的坐标(5,0),C点的坐标(0,-3),直线y=-
已知矩形OABC在平面直角坐标系中位置如图所示,A点的坐标(5,0),C点的坐标(0,-3),直线y=-| 3 |
| 4 |
(1)求点D的坐标;
(2)求经过O、A、D三点的抛物线的解析式;
(3)M是(2)中抛物线上的一个动点,N是x轴上的一个动点,是否存在以O、D、M、N为顶点,以线段OD为一边的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)令y=-3,进而代入求出x的值,即可得出D点坐标;
(2)利用O、A、D点坐标,进而利用待定系数法求二次函数解析式即可;
(3)利用平行四边形的判定与性质得出平行四边形ODM1N1,平行四边形ODN2M2和平行四边形ODN3M3中,y2=y3,进而得出答案.
(2)利用O、A、D点坐标,进而利用待定系数法求二次函数解析式即可;
(3)利用平行四边形的判定与性质得出平行四边形ODM1N1,平行四边形ODN2M2和平行四边形ODN3M3中,y2=y3,进而得出答案.
解答:解:(1)当y=-3时,-
x=-3,
解得:x=4
故D(4,-3);
(2)抛物线y=ax2+bx+c经过O、A、D点故可得出:
,
解得:
,.
故抛物线解析式为:y=
x2-
x;
(3)存在.如图,
OD=
=5,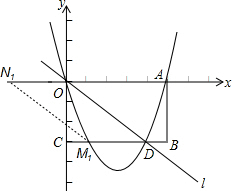
平移线段OD,当线段OD的一个端点与x轴重合,另一个端点与抛物线重合时,O、D、M、N为顶点的四边形是平行四边形,
平行四边形ODM1N1中,y1=-3,则
x2-
x=-3
解得:x1=1,x2=4
则M1(1,-3)
再由M点在x轴上方得出,平行四边形ODN2M2和平行四边形ODN3M3中,y2=y3=3,则
x2-
x=3,
解得:x2=
,x3=
,
故M2(
,3),M3(
,3)
综上所述,满足条件的M点有三个,坐标为(1,-3),(
,3),(
,3).
| 3 |
| 4 |
解得:x=4
故D(4,-3);
(2)抛物线y=ax2+bx+c经过O、A、D点故可得出:
|
解得:
|
故抛物线解析式为:y=
| 3 |
| 4 |
| 15 |
| 4 |
(3)存在.如图,
OD=
| 32+42 |

平移线段OD,当线段OD的一个端点与x轴重合,另一个端点与抛物线重合时,O、D、M、N为顶点的四边形是平行四边形,
平行四边形ODM1N1中,y1=-3,则
| 3 |
| 4 |
| 15 |
| 4 |
解得:x1=1,x2=4
则M1(1,-3)
再由M点在x轴上方得出,平行四边形ODN2M2和平行四边形ODN3M3中,y2=y3=3,则
| 3 |
| 4 |
| 15 |
| 4 |
解得:x2=
5-
| ||
| 2 |
5+
| ||
| 2 |
故M2(
5-
| ||
| 2 |
5+
| ||
| 2 |
综上所述,满足条件的M点有三个,坐标为(1,-3),(
5-
| ||
| 2 |
5+
| ||
| 2 |
点评:此题主要考查了二次函数的应用以及平行四边形的判定与性质等知识,利用平行四边形得出各边之间关系是解题关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、商家卖鞋,最关心的是鞋码的中位数 |
| B、数据2,5,7,x,3,3,6的平均数为4,则这组数据的极差是5 |
| C、要了解全市人民的低碳生活状况,适宜采用普查的方法 |
| D、随机抽查甲、乙两名同学的5次数学成绩,计算的平均分都是90分,方差分别为s甲2=5,s乙2=12,说明乙的成绩较为稳定 |
 如图,先观察图形,然后填空:
如图,先观察图形,然后填空: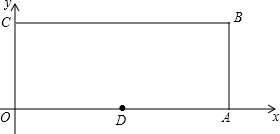 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动. 在?ABCD中,F是AD的中点,延长BC到点E,使CE=
在?ABCD中,F是AD的中点,延长BC到点E,使CE= 如图,已知:Rt△ABC中,∠C=90°,CD⊥AB于点D,AD=4,DB=2,求:BC的长.
如图,已知:Rt△ABC中,∠C=90°,CD⊥AB于点D,AD=4,DB=2,求:BC的长. 将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.
将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.