题目内容
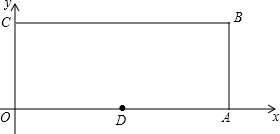 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.(1)当t为何值时,四边形PODB是平行四边形?
(2)在直线BC上是否存在一点Q,使得点O、点D、点P、点Q构成菱形?若存在,求t的值;若不存在,请说明理由.
考点:菱形的判定,坐标与图形性质,平行四边形的判定,矩形的性质
专题:
分析:(1)根据平行四边形的性质就可以知道PB=5,可以求出PC=5,从而可以求出t的值.
(2)要使ODQP为菱形,可以得出PO=5,由三角形的勾股定理就可以求出CP的值而求出t的值.
(2)要使ODQP为菱形,可以得出PO=5,由三角形的勾股定理就可以求出CP的值而求出t的值.
解答:解:(1)∵四边形PODB是平行四边形,
∴PB=OD=5,
∴PC=5,
∴t=5;
(2)∵四边形ODQP为菱形,
∴OD=OP=PQ=5,
∴在Rt△OPC中,由勾股定理得:PC=3,
∴PD=7,
∴t=7;
当点P在点Q的左侧时,此时PD=2,
∴t=2.
∴PB=OD=5,
∴PC=5,
∴t=5;
(2)∵四边形ODQP为菱形,
∴OD=OP=PQ=5,
∴在Rt△OPC中,由勾股定理得:PC=3,
∴PD=7,
∴t=7;
当点P在点Q的左侧时,此时PD=2,
∴t=2.
点评:本题考查了矩形的性质,坐标与图形的性质,平行四边形的判定及性质,菱形的判定及性质,勾股定理的运用.

练习册系列答案
相关题目
一个样本有10个数据,各数据与样本平均数的差依次为:-4,-2,5,4,-1,0,2,3,-2,-5,那么这个样本的极差和方差分别是( )
| A、10,10 |
| B、10,10.4 |
| C、10.4,10.4 |
| D、0,10.4 |
 如图,△AOB中,∠B=30°,将△AOB绕点O顺时针旋转得到△A′OB′,若∠A′=40°,则∠B′=
如图,△AOB中,∠B=30°,将△AOB绕点O顺时针旋转得到△A′OB′,若∠A′=40°,则∠B′=
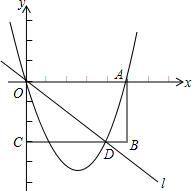 已知矩形OABC在平面直角坐标系中位置如图所示,A点的坐标(5,0),C点的坐标(0,-3),直线
已知矩形OABC在平面直角坐标系中位置如图所示,A点的坐标(5,0),C点的坐标(0,-3),直线