题目内容
 如图,已知:Rt△ABC中,∠C=90°,CD⊥AB于点D,AD=4,DB=2,求:BC的长.
如图,已知:Rt△ABC中,∠C=90°,CD⊥AB于点D,AD=4,DB=2,求:BC的长.考点:相似三角形的判定与性质
专题:
分析:由在Rt△ABC中,∠ACB=90°,CD⊥AB于D,易证得△ACD∽△CBD,然后由相似三角形的对应边成比例,求得CD的长,然后利用勾股定理,求得BC的长.
解答:解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴AD:CD=CD:BD,
∴CD=
=
=2
,
在Rt△BCD中,BC=
=2
.
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴AD:CD=CD:BD,
∴CD=
| AD•BD |
| 2×4 |
| 2 |
在Rt△BCD中,BC=
| BD2+CD2 |
| 3 |
点评:此题考查了相似三角形的判定与性质以及勾股定理.注意掌握数形结合思想的应用.

练习册系列答案
相关题目
一个圆的周长为l(l>4)cm,减少4cm后,这个圆的面积减少了( )
A、
| ||
B、
| ||
C、
| ||
D、
|
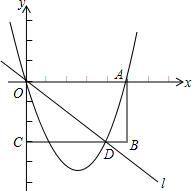 已知矩形OABC在平面直角坐标系中位置如图所示,A点的坐标(5,0),C点的坐标(0,-3),直线
已知矩形OABC在平面直角坐标系中位置如图所示,A点的坐标(5,0),C点的坐标(0,-3),直线 如图1,点A、B分别在数轴原点O的左右两侧,且
如图1,点A、B分别在数轴原点O的左右两侧,且 如图,D、E分别为线段AB、AC上一点,连接BE、CD,若AB=AC,∠B=∠C,求证:BD=CE.
如图,D、E分别为线段AB、AC上一点,连接BE、CD,若AB=AC,∠B=∠C,求证:BD=CE.