题目内容
16.某公司有某种海产品2104千克,寻求合适价格,进行8填试销,情况如下:| 第几天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 销售(元/千克) | 400 | A | 250 | 240 | 200 | 150 | 125 | 120 |
| 销售量(千克) | 30 | 40 | 48 | B | 60 | 80 | 96 | 100 |
(1)猜想函数关系式:y=$\frac{12000}{x}$.(不必写出自变量的取值范围)并写出表格中A=300B=50
(2)试销8天后,公司决定将售价定为150元/千克.则余下海产品预计20天可全部售出.
(3)按(2)中价格继续销售15天后,公司发现剩余海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新价格销售,那么新确定的价格最高不超过多少元/千克才能完成销售任务?
分析 (1)根据图中数据求出反比例函数,再分别将y=40和x=240代入求出相对应的x和y;
(2)先求出8天销售的总量和剩下的数量m,将x=150代入反比例函数中得到一天的销售量y,$\frac{m}{y}$即为所需要的天数;
(3)求出销售15天后剩余的数量除2得到后两天每天的销售量y,将y的值代入反比例函数中即可求出x.
解答 解:(1)∵xy=12000,
函数解析式为y=$\frac{12000}{x}$,
将y=40和x=240代入上式中求出相对应的x=300和y=50,
所以A=300,B=50;
(2)销售8天后剩下的数量m=2104-(30+40+48+50+60+80+96+100)=1600(千克),
当x=150时,y=$\frac{12000}{150}$=80.
∴$\frac{m}{y}$=1600÷80=20(天),
∴余下的这些海产品预计再用20天可以全部售出.
(3)1600-80×15=400(千克),400÷2=200(千克/天),
如果正好用2天售完,那么每天需要售出200千克.
当y=200时,x=$\frac{12000}{200}$=60.
如果1天售完时,当y=400时,x=30,
所以新确定的价格最高不超过60元/千克才能完成销售任务.
点评 考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
4.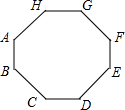 如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
 如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )| A. | 7 | B. | 8 | C. | 9 | D. | 14$\sqrt{2}$ |
11.若M(-$\frac{1}{2}$,y1)、N(-$\frac{1}{4}$,y2)、P($\frac{1}{2}$,y3)三点都在函数y=-$\frac{1}{x}$的图象上,则y1、y2、y3的大小关系为( )
| A. | y2>y3>y1 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
1.在平面直角坐标系中,点A(-2,3)关于x轴对称的对称点B的坐标为( )
| A. | (2,-3) | B. | (-2,-3) | C. | (-2,3) | D. | (2,3) |
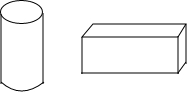 如图,某厂生产一种容积为100πL的圆柱形热水器,它的高等于底面直径d的2倍,(1L=1立方分米),厂家为它设计了一种长方体的包装盒,其容积为432L,高为6分米,且长、宽之比为2:1,问这种包装盒能用吗?
如图,某厂生产一种容积为100πL的圆柱形热水器,它的高等于底面直径d的2倍,(1L=1立方分米),厂家为它设计了一种长方体的包装盒,其容积为432L,高为6分米,且长、宽之比为2:1,问这种包装盒能用吗?