题目内容
5．
如图，AC、BD相交于点O，BE、CE分别平分∠ABD、∠ACD，且交于点E，∠A=70°，∠D=40°，求∠E的度数．
分析 根据角平分线的性质及内角与外角的关系解答即可．
解答 
解：∵BE、CE分别平分∠ABD、∠ACD，
∴∠1=∠2，∠3=∠4，
∵∠CME=∠AMB，
∴∠A+∠1=∠E+∠3①，
∵∠ENB=∠DNC，
∴∠E+∠2=∠D+∠4②，
①-②得，∠A-∠E=∠E-∠D，
则∠E=$\frac{1}{2}$（∠A+∠D）=55°．
答：∠E的度数是55°．
点评 本题考查的是三角形的外角的性质和角平分线的定义，掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
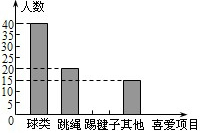某学校为了解学生大课间体育活动情况，随机抽取本校100名学生进行调查，整理收集到的数据，绘制成如图所示的统计图．若该校共有1000名学生，估计喜欢“踢毽子”的学生有250人．
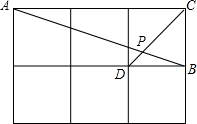如图，在边长都为1的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点P，
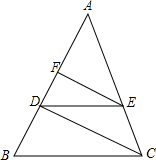如图．在△ABC中，DE∥BC，EF∥CD．求证：AD是AB和AF的比例中项．
15．下面的说法：
①三边相等的三角形是等边三角形但不是等腰三角形；
②直角三角形不是等腰三角形；
③有两个60°内角的三角形有三条对称轴；
④有这样的三角形，它有两条高线在三角形的内部，另一条高线在三角形外．
那么（ ）
①三边相等的三角形是等边三角形但不是等腰三角形；
②直角三角形不是等腰三角形；
③有两个60°内角的三角形有三条对称轴；
④有这样的三角形，它有两条高线在三角形的内部，另一条高线在三角形外．
那么（ ）
| A． | ①②③④都是正确的 | B． | 只有②③是正确的 | C． | 只有②是正确的 | D． | 只有③是正确的 |