题目内容
13.甲工程队在某工程建设中,以m元/包的价格购买本工程所需水泥共花费115万元.为加快整个工程的建设程度,甲工程队决定让出部分工程给新加入的乙工程队,甲工程队在预算中多出的水泥将以低于购买价3元/包的价格退回水泥厂(每包水泥重50千克),这样,甲工程队购买水泥的实际费用将减少65万元,此外,甲工程队施工所需的钢材、碎石等其他材料开支200万元,工人工资需要141万元,其他支出费用为材料总费用(不包含退还水泥损失的资金)的80%.在正常建设情况下,可以用水泥的使用数量来预测整个工程的盈利情况(每包水泥可创造相当于购买价的16倍的效益),经预测,甲工程队完成任务后可获得308万元的利润.①用含m的代数式表示甲工程队退还水泥所损失的资金.
②求减少工程后,甲工程队一共需要使用水泥多少吨.
分析 ①设退回了水泥x袋,则根据“退回的水泥的资金=65万元”列出代数式;
②先分别求出总效益和花费的总费用,根据利润为308万元,列出方程,求出水泥的价格,然后求出使用水泥的总吨数.
解答 解:①设退回了水泥x袋,
由题意得,115-x(m-3)=65,
解得:x=$\frac{50}{m-3}$,
则损失的资金为:3x=3×$\frac{50}{m-3}$=$\frac{150}{m-3}$(万元),
②总费用=[200+65-$\frac{150}{m-3}$]×(1+80%)+141
=(618-$\frac{270}{m-3}$)万元,
则($\frac{115}{m}$-$\frac{50}{m-3}$)×15m-(618-$\frac{270}{m-3}$)=308,
整理得:1725-$\frac{750m}{m-3}$-618+$\frac{270}{m-3}$=308,
即,849=$\frac{750m-270}{m-3}$,
解得:m=23,
经检验:m=23是原分式方程的解,且符合题意,
则共用去水泥:$\frac{115}{23}$-$\frac{50}{23-3}$=2.5(万袋),
用去水泥的重量为:2.5×1000×0.05=1250(吨).
答:减少工程后,甲工程队一共需要使用水泥1250吨.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
相关题目
3.完成下列表格,并回答问题:
(1)
由表可知方程2x2-1=0的解在0与1之间.
(2)
由表可知方程2x2-1=0的解在0.7与0.8之间.
…
以此类推,求出方程2x2-1=0的近似解.(精确到0.01)
(1)
| x | 0 | 1 | 2 |
| 2x2-1 | -1 | 1 | 7 |
(2)
| x | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| 2x2-1 | -0.5 | -0.28 | -0.2 | 0.28 | 0.62 |
…
以此类推,求出方程2x2-1=0的近似解.(精确到0.01)
2.下列数中,既是分数,又是正数的是( )
| A. | +3 | B. | -2$\frac{1}{4}$ | C. | 0 | D. | 2$\frac{3}{10}$ |
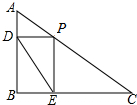 如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC点向C以2cm/s的速度移动(不与C重合),过点P作PD∥BC交AB于D,过P作PE∥AB交BC于E,若P点运动时间为t s.
如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC点向C以2cm/s的速度移动(不与C重合),过点P作PD∥BC交AB于D,过P作PE∥AB交BC于E,若P点运动时间为t s.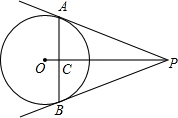 如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.
如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C. 已知a,b两数在数轴上的位置如图,化简式子:$\frac{|a|}{-a}$+$\frac{|b|}{b}$.
已知a,b两数在数轴上的位置如图,化简式子:$\frac{|a|}{-a}$+$\frac{|b|}{b}$. 如图,点O是△ABC的两条角平分线的交点,过O作AO的垂线交AB于D,求证:△OBD∽△CBO.
如图,点O是△ABC的两条角平分线的交点,过O作AO的垂线交AB于D,求证:△OBD∽△CBO. 如图,AC、BD相交于点O,BE、CE分别平分∠ABD、∠ACD,且交于点E,∠A=70°,∠D=40°,求∠E的度数.
如图,AC、BD相交于点O,BE、CE分别平分∠ABD、∠ACD,且交于点E,∠A=70°,∠D=40°,求∠E的度数.