题目内容
10．解方程：$\frac{1}{\sqrt{x}（\sqrt{x}+2）}$+$\frac{1}{（\sqrt{x}+2）（\sqrt{x}+4）}$+…+$\frac{1}{（\sqrt{x}+8）（\sqrt{x}+10）}$=$\frac{5}{24}$．分析 首先拆分$\frac{1}{\sqrt{x}（\sqrt{x}+2）}$=$\frac{1}{2}$（$\frac{1}{\sqrt{x}}$-$\frac{1}{\sqrt{x}+2}$），$\frac{1}{（\sqrt{x}+2）（\sqrt{x}+4）}$=$\frac{1}{2}$（$\frac{1}{\sqrt{x}+2}$-$\frac{1}{\sqrt{x}+4}$），…$\frac{1}{（\sqrt{x}+8）（\sqrt{x}+10）}$=$\frac{1}{2}$（$\frac{1}{\sqrt{x}+8}$-$\frac{1}{\sqrt{x}+10}$），进一步代换求得答案即可．
解答 解：$\frac{1}{\sqrt{x}（\sqrt{x}+2）}$+$\frac{1}{（\sqrt{x}+2）（\sqrt{x}+4）}$+…+$\frac{1}{（\sqrt{x}+8）（\sqrt{x}+10）}$=$\frac{5}{24}$
$\frac{1}{2}$×（$\frac{1}{\sqrt{x}}$-$\frac{1}{\sqrt{x}+2}$+$\frac{1}{\sqrt{x}+2}$-$\frac{1}{\sqrt{x}+4}$+…+$\frac{1}{\sqrt{x}+8}$-$\frac{1}{\sqrt{x}+10}$=$\frac{5}{24}$
$\frac{1}{\sqrt{x}}$-$\frac{1}{\sqrt{x}+10}$=$\frac{5}{12}$
$\frac{10}{\sqrt{x}（\sqrt{x}+10）}$=$\frac{5}{12}$
$\sqrt{x}$（$\sqrt{x}+10$）=24
（$\sqrt{x}$+12）（$\sqrt{x}$-2）=0，
$\sqrt{x}$=-12（无解），$\sqrt{x}$=2，
x=4．
点评 此题考查二次根式的运用，根据算式的特点，利用二次根式拆分是解决问题的关键．
名校课堂系列答案
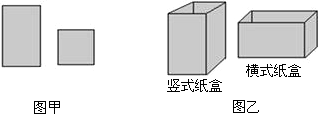
（1）现有正方形纸板150张，长方形纸板300张，设做竖式纸盒x个，横式纸盒y个，
①根据题意，完成以下表格：
| 竖式纸盒（个） | 横式纸盒（个） | |
| x | y | |
| 正方形纸板（张） | x | 2y |
| 长方形纸板（张） | 4x | 3y |
（2）若有正方形纸板32张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完，已知70＜a＜75．则a的值是73．
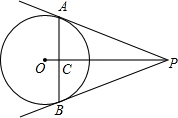如图，PA、PB是⊙O的切线，切点分别为A、B，OP交AB于点C．
如图，点O是△ABC的两条角平分线的交点，过O作AO的垂线交AB于D，求证：△OBD∽△CBO．
如图，AC、BD相交于点O，BE、CE分别平分∠ABD、∠ACD，且交于点E，∠A=70°，∠D=40°，求∠E的度数．| A． | +3 | B． | -2$\frac{1}{4}$ | C． | 0 | D． | 2$\frac{3}{10}$ |