题目内容
13.小斌在不过河的情况下,测量河对岸一座信号发射塔的高度,他用高1米的测角仪AD在河岸这边的D处测得信号发射的顶端C的角为45°,再向信号发射塔方向前进30米,又测得信号发射塔的顶端C的仰角为60°,求这个信号发射塔的高度.(结果保留根号)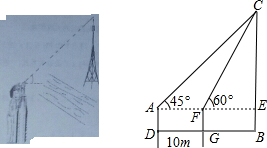
分析 在直角△EAC和直角△CEF中,根据三角函数可以用CE把AE、EF表示出来,根据AF=DG=30米,就可以得到一个关于CE的方程,求出CE的值,再根据AD的值,即可求出BC.
解答  解:在直角三角形EAC中,
解:在直角三角形EAC中,
∵∠EAC=45°,
∴AE=CE,
设CE=x米,
在直角三角形CEF中,
∵∠EFC=60°,
∴∠FCE=30°,
∴MN=CE•tan30°=$\frac{\sqrt{3}}{3}$x,
∵AF=DG=30米,
∴30+$\frac{\sqrt{3}}{3}$x=x,
解得:x=45+15$\sqrt{3}$,
∵AD=1米,
∴BC=BE+CE=46+15$\sqrt{3}$(米);
答:这个信号发射塔的高度为(46+15$\sqrt{3}$)米.
点评 本题主要考查了解直角三角的应用-仰角俯角,用到的知识点是三角函数的定义,根据三角函数可以把问题转化为方程问题来解决是关键.

练习册系列答案
相关题目
5.已知正方形ABCD的边长为2,若a<AC<b,其中a和b为连续的正整数,则ab的值为( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
 完成下列推理填空:
完成下列推理填空: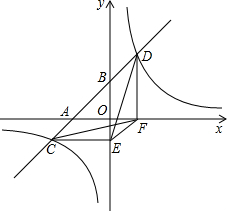 如图,直线l与x轴、y轴交于A、B两点.与双曲线y=$\frac{k}{x}$和交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F.连接CF、DE.则下列结论中:
如图,直线l与x轴、y轴交于A、B两点.与双曲线y=$\frac{k}{x}$和交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F.连接CF、DE.则下列结论中:
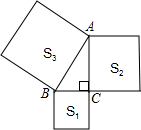 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=10,S2=15,则AB的长为5.
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=10,S2=15,则AB的长为5.