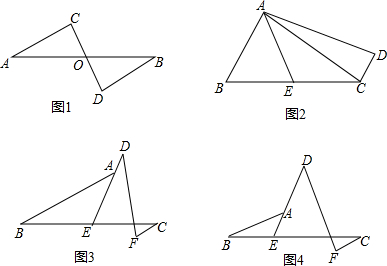
题目内容
7.如图1,线段AB与线段CD的中点重合,根据“边角边”可以得到△ACO≌△BDO,进一步可以得到对应的边相等,对应的角相等.(1)问题探究:
①如图2,在四边形ABCD中,AB∥CD,点E为BC的中点,∠BAE=∠EAD,试探究AB与AD、CD之间的等量关系,并证明你的结论;
②如图3,DE、BC相交于点E,BA交DE于点A,点E是BC的中点,且∠BAE=∠EDF,CF∥AB,试探究AB与DE、CF之间的等量关系,并证明你的结论;
(2)拓展延伸
①如图4,DE、BC相交于点E,BA交DE于点A,且BE:EC=1:2,∠BAE=∠EDF,CF∥AB,试探究AB与DF、CF之间的等量关系,并证明你的结论:
②如图所示,DE、BC相交于点E,BA交DE于点A,且BE:EC=1:n,∠BAE=∠EDF,CF∥AB,直接写出AB与DF、CF之间的等量关系.
分析 (1)①结论:AD=AB+CD.如图2中延长AE、DC交于点F,只要证明△ABE≌△FCE以及DA=DF即可.
结论DF=AB-CF,如图3中延长DE、CF交于点G,只要证明△ABE≌△GCE,以及DF=FG即可.
(2)①结论:DF=2•AB-CF,如图4中,延长DE、CF交于点G,只要证明△ABE∽△GCE以及DF=FG;
②结论:DF=n•AB-CF证明方法类似①.
解答 解:(1)①结论:AD=AB+CD.理由如下,
如图2中,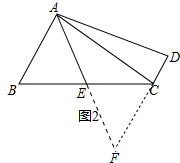 延长AE、DC交于点F.
延长AE、DC交于点F.
∵AB∥CF,
∴∠B=∠ECF,
在△ABE和△FCE中,
$\left\{\begin{array}{l}{∠B=∠ECF}\\{BE=EC}\\{∠AEB=∠FEC}\end{array}\right.$,
∴△ABE≌△FCE,
∴AB=CF,∠BAE=∠F=∠DAF
∴DA=DF,
∴AD=DC+CF=CD+AB.
②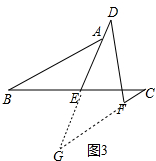 结论:DF=AB-CF,理由如下,
结论:DF=AB-CF,理由如下,
如图3中,延长DE、CF交于点G.
∵AB∥CF,
∴∠B=∠C,
在△ABE和△GCE中,
$\left\{\begin{array}{l}{∠B=∠C}\\{BE=EC}\\{∠AEB=∠GEC}\end{array}\right.$,
∴△ABE≌△GCE,
∴AB=CG,∠BAE=∠G=∠GDF,
∴DF=FG,
∴DF=GC-CF=AB-AF.
(2)①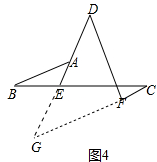 结论:DF=2•AB-CF.理由如下,
结论:DF=2•AB-CF.理由如下,
如图4中,延长DE、CF交于点G,
∵AB∥GC,
∴△ABE∽△GCE,
∴$\frac{AB}{GC}$=$\frac{BE}{EC}$=$\frac{1}{2}$.∠BAE=∠G=∠GDF,
∴DF=FG,GC=2•AB,
∴DF=CG-CF=2•AB-CF.
②结论:DF=n•AB-CF.理由如下,
如图4中,延长DE、CF交于点G,
∵AB∥GC,
∴△ABE∽△GCE,
∴$\frac{AB}{GC}$=$\frac{BE}{EC}$=$\frac{1}{n}$.∠BAE=∠G=∠GDF,
∴DF=FG,GC=n•AB
∴DF=CG-CF=n•AB-CF.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是倍长中线添加辅助线,构造全等三角形,属于中考常考题型.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案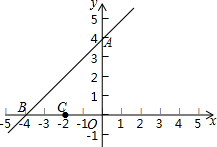 如图,已知直线l的解析式为y=x+4与y轴交于A点,与x轴交于B点.
如图,已知直线l的解析式为y=x+4与y轴交于A点,与x轴交于B点.
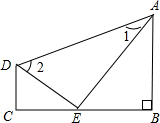 如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,试判断DC与BC的位置关系,并加以说明.
如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,试判断DC与BC的位置关系,并加以说明.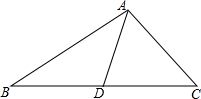 如图,AD是△ABC的中线,∠CAD=60°,AD=4,AB-AC=2,则BC的长为2$\sqrt{21}$.
如图,AD是△ABC的中线,∠CAD=60°,AD=4,AB-AC=2,则BC的长为2$\sqrt{21}$.