题目内容
8.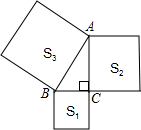 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=10,S2=15,则AB的长为5.
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=10,S2=15,则AB的长为5.
分析 先设Rt△ABC的三边分别为a、b、c,再分别用a、b、c表示S1、S2、S3的值,由勾股定理即可得出S3的值.
解答 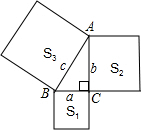 解:设Rt△ABC的三边分别为a、b、c,
解:设Rt△ABC的三边分别为a、b、c,
∴S1=a2=10,S2=b2=15,S3=c2,
∵△ABC是直角三角形,
∴a2+b2=c2,即S1+S2=S3,
∴S3=S1+S2=10+15=25,
则AB=c=5.
故答案是:5.
点评 本题考查的是勾股定理的应用及正方形的面积公式,熟知勾股定理是解答此题的关键.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
19.在①x2-22=(x+2)(x-2);②(2a+b)2=4a2+b2;③($\frac{1}{8}$×10)0=1;④(m+2)(m-4)=m2-8中,其中正确的算式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.将函数y=-3x的图象沿y轴向下平移2个单位长度后,所得图象对应的函数关系式为( )
| A. | y=3x+2 | B. | y=-3x-2 | C. | y=-3(x+2) | D. | y=-3(x-2) |
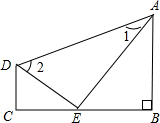 如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,试判断DC与BC的位置关系,并加以说明.
如图,AE平分∠BAD,DE平分∠ADC,AB⊥BC于B,∠1+∠2=90°,试判断DC与BC的位置关系,并加以说明.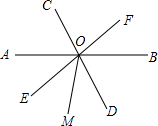 如图,直线AB,CD,EF相交于点O,∠BOD=64°,∠AOF=140°.
如图,直线AB,CD,EF相交于点O,∠BOD=64°,∠AOF=140°.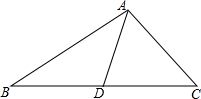 如图,AD是△ABC的中线,∠CAD=60°,AD=4,AB-AC=2,则BC的长为2$\sqrt{21}$.
如图,AD是△ABC的中线,∠CAD=60°,AD=4,AB-AC=2,则BC的长为2$\sqrt{21}$.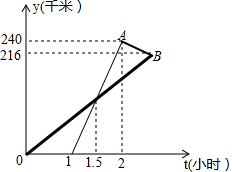 十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A,然后乘出租车去游乐园B(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y(千米)与小明乘车时间t(时)的函数图象如图所示.
十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A,然后乘出租车去游乐园B(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y(千米)与小明乘车时间t(时)的函数图象如图所示.