题目内容
如图，已知在平行四边形ABCD中，点E在边BC上，射线AE交DC的延长线于点F，AB=2，BE=3EC，那么DF的长为考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：如图，证明AB∥CD，CD=AB=2，得到△ABE∽△FCE，列出比例式求出CF的长度，即可解决问题．
解答：解：如图，∵四边形ABCD为平行四边形，
∴AB∥CD，CD=AB=2；
∴△ABE∽△FCE，
∴
=
=
，
∴CF=
，DF=2+
=
，
故答案为
．
解：如图，∵四边形ABCD为平行四边形，∴AB∥CD，CD=AB=2；
∴△ABE∽△FCE，
∴
| AB |
| CF |
| BE |
| CE |
| 3CE |
| CE |
∴CF=
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
故答案为
| 8 |
| 3 |
点评：该题主要考查了平行四边形的性质、相似三角形的判定及其性质的应用问题；应牢固掌握平行四边形的性质、相似三角形的判定及其性质等知识点．
练习册系列答案
应用题作业本系列答案
相关题目
如图，已知AC平分∠DAB，E为AC上一点，AD=AB，那么△CDE≌△CBE，为什么？如果方程1=3-2x与关于x的方程2=
的解相同，则a的值为（ ）
| a-x |
| 3 |
| A、1 | ||
| B、3 | ||
| C、7 | ||
D、
|
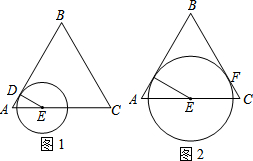己知等边△ABC，边长为4，点D从点A出发，沿AB运动到点B，到点B停止运动．点E从A出发，沿AC的方向在直线AC上运动．点D的速度为每秒1个单位，点E的速度为每秒2个单位，它们同时出发，同时停止．以点E为圆心，DE长为半径作圆．设E点的运动时间为t秒，
在截面为半圆形的水槽内装有一些水，如图．水面宽AB为6分米，如果再注入一些水后，水面AB上升1分米，水面宽变为8分米，则该水槽截面直径为（ ）| A、5分米 | B、6分米 |
| C、8分米 | D、10分米 |
有理数a、b在数轴上的位置如图所示，在下列结论中：
如图，已知AB=DB，要使△ABC≌△DBC，还要添加什么条件？添加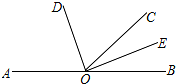
如图，点A、O、B在同一条直线上，射线OD与射线OE分别平分∠AOC和∠BOC