题目内容
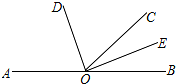 如图,点A、O、B在同一条直线上,射线OD与射线OE分别平分∠AOC和∠BOC
如图,点A、O、B在同一条直线上,射线OD与射线OE分别平分∠AOC和∠BOC(1)若∠BOE=20°,则∠AOD的度数为
(2)若∠AOD=4∠BOE,求∠AOD的度数.
考点:角平分线的定义
专题:
分析:(1)由射线OE平分∠BOC,根据角平分线定义得出∠BOC=2∠BOE=40°,根据邻补角定义得到∠AOC=180°-∠BOC=140°,再由射线OD平分∠AOC,得出∠AOD=
∠AOC=70°;
(2)设∠BOE=x,则∠AOD=4∠BOE=4x.根据角平分线定义得出∠BOC=2∠BOE=2x,∠AOC=2∠AOD=8x.由邻补角定义得到∠AOC+∠BOC=180°,即8x+2x=180°,解方程求出x的值,进而得到∠AOD的度数.
| 1 |
| 2 |
(2)设∠BOE=x,则∠AOD=4∠BOE=4x.根据角平分线定义得出∠BOC=2∠BOE=2x,∠AOC=2∠AOD=8x.由邻补角定义得到∠AOC+∠BOC=180°,即8x+2x=180°,解方程求出x的值,进而得到∠AOD的度数.
解答:解:(1)∵射线OE平分∠BOC,∠BOE=20°,
∴∠BOC=2∠BOE=40°,
∴∠AOC=180°-∠BOC=140°,
∵射线OD平分∠AOC,
∴∠AOD=
∠AOC=70°.
故答案为70°;
(2)设∠BOE=x,则∠AOD=4∠BOE=4x.
∵射线OE平分∠BOC,
∴∠BOC=2∠BOE=2x.
∵射线OD平分∠AOC,
∴∠AOC=2∠AOD=8x.
∵∠AOC+∠BOC=180°,
∴8x+2x=180°,
∴x=18°,
∴∠AOD=4×18°=72°.
∴∠BOC=2∠BOE=40°,
∴∠AOC=180°-∠BOC=140°,
∵射线OD平分∠AOC,
∴∠AOD=
| 1 |
| 2 |
故答案为70°;
(2)设∠BOE=x,则∠AOD=4∠BOE=4x.
∵射线OE平分∠BOC,
∴∠BOC=2∠BOE=2x.
∵射线OD平分∠AOC,
∴∠AOC=2∠AOD=8x.
∵∠AOC+∠BOC=180°,
∴8x+2x=180°,
∴x=18°,
∴∠AOD=4×18°=72°.
点评:此题主要考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.同时考查了邻补角定义及方程思想.

练习册系列答案
相关题目
 一个实物的三视图如图,则这个实物形状可能是( )
一个实物的三视图如图,则这个实物形状可能是( )| A、圆柱 | B、三棱柱 |
| C、四棱柱 | D、五棱柱 |
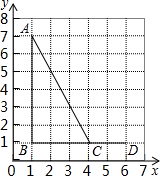 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,0),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,0),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )| A、(6,0) |
| B、(6,3) |
| C、(6,5) |
| D、(4,2) |
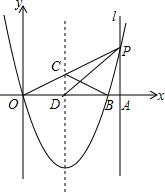 直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.
直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m. 如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交DC的延长线于点F,AB=2,BE=3EC,那么DF的长为
如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交DC的延长线于点F,AB=2,BE=3EC,那么DF的长为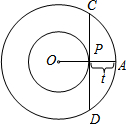 如图,已知OA=4cm,一个动点P从A向O以1cm/秒的速度运动,以O为圆心,分别以OA、OP为半径画大圆和小圆,以P为切点的小圆的切线与大圆交于C、D,则弦CD的长y(cm)关于P的运动时间t(秒)的函数解析式为
如图,已知OA=4cm,一个动点P从A向O以1cm/秒的速度运动,以O为圆心,分别以OA、OP为半径画大圆和小圆,以P为切点的小圆的切线与大圆交于C、D,则弦CD的长y(cm)关于P的运动时间t(秒)的函数解析式为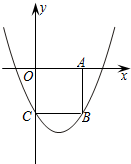 如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=
如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=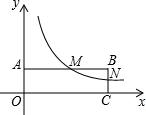 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA、OC为边作矩形OABC,双曲线
如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA、OC为边作矩形OABC,双曲线