题目内容
4.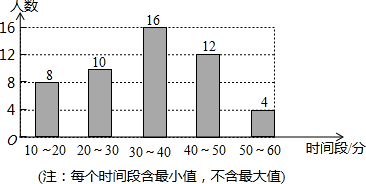 某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.
某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.(1)求样本容量,并估计全校同学在周末期间平均每夭做家务活的时间在40分钟以上(含40分钟)的人数;
(2)校学生会拟在表现突出的A、B、C、D四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到A、B两名同学的概率.
分析 (1)把各时间段的学生人数相加即可;用全校同学的人数乘以40分钟以上(含40分钟)的人数所占的比重,计算即可得解;
(2)列出图表,然后根据概率公式计算即可得解.
解答 解:(1)8+10+16+12+4=50人,
1000×$\frac{12+4}{50}$=320人;
(2)列表如下:
共有12种情况,恰好抽到A、B两名同学的是2种,
所以P(恰好抽到A、B名同学)=$\frac{2}{12}=\frac{1}{6}$.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力,列表法与树状图,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
相关题目
14.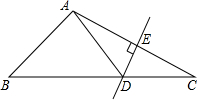 如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )
如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )
 如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )
如图所示,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为( )| A. | 16cm | B. | 19cm | C. | 21cm | D. | 25cm |
 将两块全等的含30°角的三角尺按如图的方式摆放在一起.求证:四边形ABCD是平行四边形.
将两块全等的含30°角的三角尺按如图的方式摆放在一起.求证:四边形ABCD是平行四边形.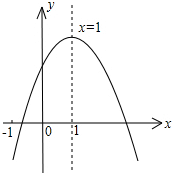 已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论:①abc<0;②4a+2b+c>0;③b2-4ac<0;④b>a+c;⑤a+2b+c>0,其中正确的结论有①②④⑤.
已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论:①abc<0;②4a+2b+c>0;③b2-4ac<0;④b>a+c;⑤a+2b+c>0,其中正确的结论有①②④⑤. 甲乙两人共同加工一批零件,从工作开始到加工完这批零件两人恰好同时工作6小时,二人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图象如图所示,根据信息回答下列问题:
甲乙两人共同加工一批零件,从工作开始到加工完这批零件两人恰好同时工作6小时,二人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图象如图所示,根据信息回答下列问题: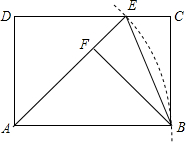 如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.
如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.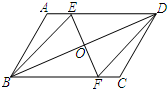 如图,在平行四边形ABCD中,BD的垂直平分线EF与AD交于点E,与BC交于点F,与BD交于点O.
如图,在平行四边形ABCD中,BD的垂直平分线EF与AD交于点E,与BC交于点F,与BD交于点O.