题目内容
16.计算:(1)$\sqrt{12}$-2sin60°+($\frac{1}{2}$)-1-|1-$\sqrt{3}$|;
(2)$\frac{x-3}{x-2}$÷(x+2-$\frac{5}{x-2}$).
分析 (1)原式第一项化为最简二次根式,第二项利用特殊角的三角函数值计算,第三项利用负整数指数幂法则计算,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=2$\sqrt{3}$-2×$\frac{\sqrt{3}}{2}$+2-$\sqrt{3}$+1=3;
(2)原式=$\frac{x-3}{x-2}$÷$\frac{(x+2)(x-2)-5}{x-2}$=$\frac{x-3}{x-2}$•$\frac{x-2}{(x+3)(x-3)}$=$\frac{1}{x+3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.下列调查中,不适合采用全面调查方式的是( )
| A. | 了解全班同学每周进行体育锻炼的时间 | |
| B. | 对旅客上飞机前进行的安检 | |
| C. | 学校招聘教师,对应聘人员进行面试 | |
| D. | 了解全市中小学生每天的零花钱 |
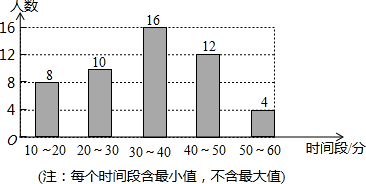 某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.
某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图. 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.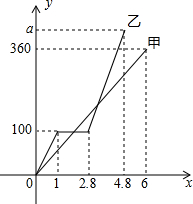 甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率提高了50%.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率提高了50%.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.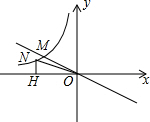 如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.
如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H. 如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.
如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.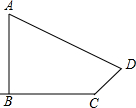 如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=12m,斜坡坡面上的影长CD=4m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.(结果保留一位小数,参考数据:$\sqrt{3}$≈1.732).
如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=12m,斜坡坡面上的影长CD=4m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.(结果保留一位小数,参考数据:$\sqrt{3}$≈1.732).