题目内容
13.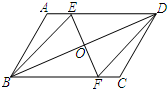 如图,在平行四边形ABCD中,BD的垂直平分线EF与AD交于点E,与BC交于点F,与BD交于点O.
如图,在平行四边形ABCD中,BD的垂直平分线EF与AD交于点E,与BC交于点F,与BD交于点O.(1)证明:OE=OF;
(2)证明:四边形BEDF是菱形.
分析 (1)根据平行四边形的性质和ASA证明△ODE与△OBF全等,再利用全等三角形的性质证明即可;
(2)根据菱形的判定解答即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴OD=OB,AD∥BC,
∴∠EDB=∠FBD,
又∵∠EOD=∠FOB,
在△ODE与△OBF中,
$\left\{\begin{array}{l}{∠EOD=∠FOB}\\{OD=OB}\\{∠EDB=∠FBD}\end{array}\right.$,
∴△ODE≌△OBF,
∴OE=OF;
(2)∵EF⊥BD,
∴四边形EBFD的对角线垂直互相平分,
∴四边形EBFD是菱形.
点评 此题考查菱形的判定,关键是根据ASA证明△ODE与△OBF全等.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
3.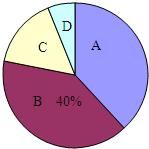 某市共有15000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:
某市共有15000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:
请你根据以上图表提供的信息,解答下列问题:
(1)m=20,n=8,x=0.4,y=0.16;
(2)在扇形图中,C等级所对应的圆心角是57.6度;
(3)如果该校九年级共有300名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
 某市共有15000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:
某市共有15000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | 0.38 |
| B | 75~89 | m | x |
| C | 60~74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(1)m=20,n=8,x=0.4,y=0.16;
(2)在扇形图中,C等级所对应的圆心角是57.6度;
(3)如果该校九年级共有300名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
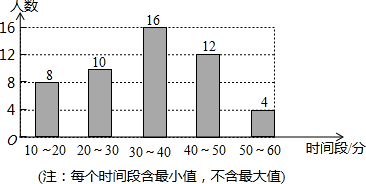 某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.
某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.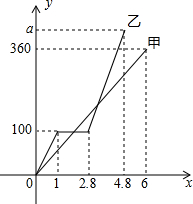 甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率提高了50%.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率提高了50%.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.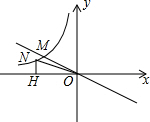 如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.
如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.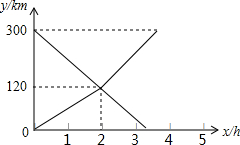 甲、乙两车分别从A,B两地同时出发,沿一条公路相向而行,2小时后两车相遇,相遇后乙车速度变为90km/h,而甲车速度保持不变,甲、乙两车离B地路程为y甲(km)、y乙(km),行驶时间为x(h),y甲、y乙与x之间的函数图象如图所示.
甲、乙两车分别从A,B两地同时出发,沿一条公路相向而行,2小时后两车相遇,相遇后乙车速度变为90km/h,而甲车速度保持不变,甲、乙两车离B地路程为y甲(km)、y乙(km),行驶时间为x(h),y甲、y乙与x之间的函数图象如图所示. 如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.
如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.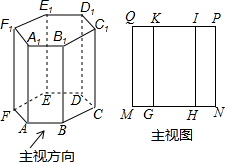 如图为一个几何体和它的主视图,请完成下面填空.
如图为一个几何体和它的主视图,请完成下面填空.