题目内容
12. 甲乙两人共同加工一批零件,从工作开始到加工完这批零件两人恰好同时工作6小时,二人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图象如图所示,根据信息回答下列问题:
甲乙两人共同加工一批零件,从工作开始到加工完这批零件两人恰好同时工作6小时,二人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图象如图所示,根据信息回答下列问题:(1)求甲在前4个小时的工作效率;
(2)求线段CD所在直线的解析式和这批零件的总数;
(3)加工多长时间,甲乙两人各自加工的零件个数相差5个?
分析 (1)根据工作效率=生产总数÷时间,即可得出结论;
(2)设线段CD所在直线的解析式为y=kx+b,设线段AB所在直线的解析式为y1=k1x+b1.结合图象找出点的坐标利用待定系数法即可求出直线CD、AB的解析式,分别求出当x=6时的y值,两值相加即可得出结论;
(3)根据函数图象找出线段OC所在的直接解析式,分段考虑二者之差为5时的情况,利用图象在上面的函数解析式-图象在下面的函数解析式=5,可得出关于x的一元一次方程,解方程即可得出结论.
解答 解:(1)甲在前4个小时每小时生产零件数为:80÷4=20(个),
∴甲在前4个小时的工作效率为20个/小时.
(2)设线段CD所在直线的解析式为y=kx+b,
将点(2,80)、(5,110)代入到y=kx+b中,
得$\left\{\begin{array}{l}{80=2k+b}\\{110=5k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=10}\\{b=60}\end{array}\right.$.
∴直线CD解析式为y=10x+60.
当x=6时,y=120.
设线段AB所在直线的解析式为y1=k1x+b1,
将点(4,80)、(5,110)代入到y1=k1x+b1中,
得$\left\{\begin{array}{l}{80=4{k}_{1}+{b}_{1}}\\{110=5{k}_{1}+{b}_{1}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=30}\\{{b}_{1}=-40}\end{array}\right.$.
∴直线AB解析式为y1=30x-40.
当x=6时,y1=140.
∵120+140=260(个).
∴这批零件的总数为260个.
(3)设工作x(x<4)小时后,甲乙两人各自加工的零件个数相差5个,
根据图象得:40x-20x=5,解得:x=$\frac{1}{4}$;
当x>4时,分两种情况:
y-y1=5时,即(10x+60)-(30x-40)=5,解得:x=$\frac{19}{4}$;
y1-y=5时,即(30x-40)-(10x+60)=5,解得x=$\frac{21}{4}$.
答:加工时间为$\frac{1}{4}$、$\frac{19}{4}$或$\frac{21}{4}$小时时,甲乙两人各自加工的零件个数相差5个.
点评 本题考查了一次函数的应用以及待定系数法求函数解析式,解题的关键是:(1)利用数量关系直接求值即可;(2)利用待定系数法求出函数解析式;(3)分段考虑根据图象的关系得出关于x的方程.本题属于基础题,难度不大,解决该题型题目时,结合图象上点的坐标,利用待定系数法求出函数解析式是关键.

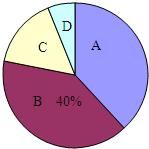 某市共有15000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:
某市共有15000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | 0.38 |
| B | 75~89 | m | x |
| C | 60~74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(1)m=20,n=8,x=0.4,y=0.16;
(2)在扇形图中,C等级所对应的圆心角是57.6度;
(3)如果该校九年级共有300名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
| A. | 了解全班同学每周进行体育锻炼的时间 | |
| B. | 对旅客上飞机前进行的安检 | |
| C. | 学校招聘教师,对应聘人员进行面试 | |
| D. | 了解全市中小学生每天的零花钱 |
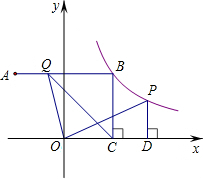 在平面直角坐标系中,点A(-3,4)关于y轴的对称点为点B,连接AB,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
在平面直角坐标系中,点A(-3,4)关于y轴的对称点为点B,连接AB,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.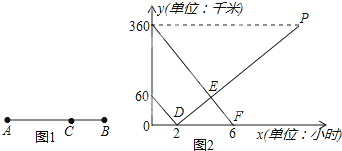
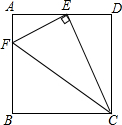 如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF=$\frac{1}{2}$.
如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF=$\frac{1}{2}$.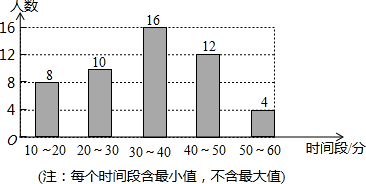 某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.
某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.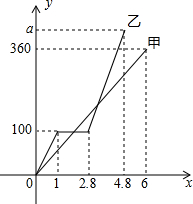 甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率提高了50%.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率提高了50%.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.