题目内容
9.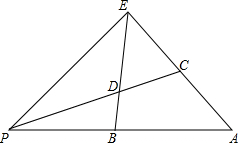 如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.
如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.
分析 根据等腰三角形的性质得到∠EDC=∠ECD,由邻补角的定义得到∠EDP=∠ACB,推出△EDP∽△ACP,根据相似三角形的性质得到$\frac{PE}{PA}=\frac{DE}{AC}$,等量代换得到结论.
解答 证明:∵ED=EC,
∴∠EDC=∠ECD,
∴∠EDP=∠ACP,
∵∠PEB=∠A,
∴△EDP∽△ACP,
∴$\frac{PE}{PA}=\frac{DE}{AC}$,
∴PA•DE=AC•PE,
∴PA•CE=AC•PE.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,邻补角的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
18.某次篮球联赛积分
(1)求胜一场、负一场积分各是多少?
(2)某队胜场总积分能等于它的负场总积分?
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 东方 | 10 | 4 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 蓝天 | 14 | 9 | 5 | 23 |
| 雄鹰 | 14 | 7 | 7 | 21 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
(2)某队胜场总积分能等于它的负场总积分?
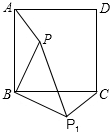 如图,点P是正方形ABCD内一点,将△ABP绕点B按顺时针方向旋转至与△CBP1重合,若PB=4cm,则PP1=4$\sqrt{2}$cm.
如图,点P是正方形ABCD内一点,将△ABP绕点B按顺时针方向旋转至与△CBP1重合,若PB=4cm,则PP1=4$\sqrt{2}$cm.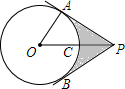 如图,PA,PB分别与⊙O相切于A,B两点,PO交⊙O于点C,PC=OC,AP=4$\sqrt{3}$cm.
如图,PA,PB分别与⊙O相切于A,B两点,PO交⊙O于点C,PC=OC,AP=4$\sqrt{3}$cm.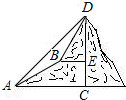 已知:如图,在山脚的A处测得山顶D的仰角为45°,沿着坡度为30°的斜角前进400米处到B处(即∠BAC=30°,AB=400米),测得D的仰角为60°,求山的高度CD.
已知:如图,在山脚的A处测得山顶D的仰角为45°,沿着坡度为30°的斜角前进400米处到B处(即∠BAC=30°,AB=400米),测得D的仰角为60°,求山的高度CD.