题目内容
20.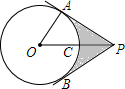 如图,PA,PB分别与⊙O相切于A,B两点,PO交⊙O于点C,PC=OC,AP=4$\sqrt{3}$cm.
如图,PA,PB分别与⊙O相切于A,B两点,PO交⊙O于点C,PC=OC,AP=4$\sqrt{3}$cm.(1)求⊙O的半径;
(2)求图中阴影部分的面积.
分析 (1)根据切线的性质得到∠OAP=90°,由已知条件得到OA=$\frac{1}{2}$OP,证得∠APO=30°,解直角三角形得到AP=4$\sqrt{3}$cm,即可得到结论;
(2)连接OB,根据切线的性质得到∠APB=2∠APO=60°,∠OAP=∠OBP=90°,根据四边形的内角和得到∠AOB=120°,于是得到结论.
解答  解:(1)∵PA,PB分别与⊙O相切于A,B两点,
解:(1)∵PA,PB分别与⊙O相切于A,B两点,
∴∠OAP=90°,
∵PC=OC,
∴OA=$\frac{1}{2}$OP,
∴∠APO=30°,
∵AP=4$\sqrt{3}$,
∴OA=4cm,
∴⊙O的半径=4cm;
(2)连接OB,
∵PA,PB分别与⊙O相切于A,B两点,
∴∠APB=2∠APO=60°,∠OAP=∠OBP=90°,
∴∠AOB=120°,
∴S阴影=四边形AOBP-S扇形=4×4$\sqrt{3}$-$\frac{120•π×{4}^{2}}{360}$=(16$\sqrt{3}$-$\frac{16}{3}$π)cm2.
点评 此题考查了切线长定理,直角三角形的性质,扇形面积公式等知识,熟记切线长定理是解题的关键.

练习册系列答案
相关题目
5. 如图中小于平角的角的个数为( )
如图中小于平角的角的个数为( )
 如图中小于平角的角的个数为( )
如图中小于平角的角的个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
 已知一次函数y=kx+b的图象如图所示,
已知一次函数y=kx+b的图象如图所示, 如图,∠ABD=∠BCD=90°,AB=4,sinA=$\frac{3}{5}$,CD=2,求∠CBD的三个三角函数值.
如图,∠ABD=∠BCD=90°,AB=4,sinA=$\frac{3}{5}$,CD=2,求∠CBD的三个三角函数值.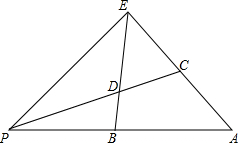 如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.
如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.