题目内容
4.在?ABCD中,∠A的平分线分CD为4和5两段,cos∠A=$\frac{3}{5}$,则?ABCD的面积为36或$\frac{144}{5}$cm2.分析 根据题意画出图形,分两种情况讨论:(1)当DF=5m时;(2)当DF=4m时.证出AD=DF,求出AD的长,根据三角函数和勾股定理求出DE的长,计算面积即可.
解答  解:(1)如图1,当DF=5m时,
解:(1)如图1,当DF=5m时,
∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
∴AD=DF=5m,
∵cos∠DAB=$\frac{3}{5}$,
∴$\frac{AE}{AD}$=$\frac{3}{5}$,
∴$\frac{AE}{5}$=$\frac{3}{5}$,
∴AE=3,
在Rt△AED中,DE=$\sqrt{{5}^{2}-{3}^{3}}$=4,
S平行四边形ABCD=9×4=36cm2.
(2)如图2,当DF=4m时,
∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
∴AD=DF=4m,
∵cos∠DAB=$\frac{3}{5}$,
∴$\frac{AE}{AD}$=$\frac{3}{5}$,
∴$\frac{AE}{4}$=$\frac{3}{5}$,
∴AE=$\frac{12}{5}$,
在Rt△AED中,DE=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,
S平行四边形ABCD=9×$\frac{16}{5}$=$\frac{144}{5}$cm2.
故答案为36或$\frac{144}{5}$cm2.
点评 本题考查了平行四边形的性质,涉及勾股定理、三角函数、等腰三角形的性质等知识,要注意分类讨论.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
14.A、B两地相距870千米,有两列火车同时从两站相对开出,甲车每小时行60千米,乙车每小时比甲车快5千米,6小时后两车的距离为( )
| A. | 80千米 | B. | 90千米 | C. | 100千米 | D. | 120千米 |
6.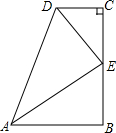 在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
 在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
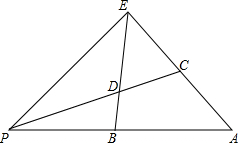 如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.
如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.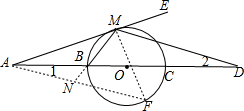 如图,在同一直线上顺次取AB=BC=CD,以BC为直径作⊙O,从A点作⊙O的切线AE,切点为M,求证:∠AMB=∠EMD.
如图,在同一直线上顺次取AB=BC=CD,以BC为直径作⊙O,从A点作⊙O的切线AE,切点为M,求证:∠AMB=∠EMD.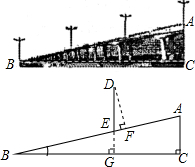 如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).
如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°,求路灯DE的顶端D点到桥面AB的垂直距离(即DF的长,精确到0.1m).