题目内容
11.解方程:(1)x(x-3)=15-5x
(2)x2-2x-4=0
(3)x2+2x-5=0(请用配方法解)
分析 (1)移项,整理,利用因式分解法求得方程的解;
(2)(3)利用配方法求得方程的解即可.
解答 解:(1)x(x-3)=15-5x
x(x-3)+5(x-3)=0
(x-3)(x+5)=0
x-3=0,x+5=0
解得:x1=3,x2=-5;
(2)x2-2x-4=0
x2-2x=4
x2-2x+1=5
(x-1)2=5
x-1=±$\sqrt{5}$
解得:x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$;
(3)x2+2x-5=0
x2+2x=5
x2+2x+1=6
(x+1)2=6
x+1=±$\sqrt{6}$
解得:x1=-1+$\sqrt{6}$,x2=-1-$\sqrt{6}$.
点评 此题考查解一元二次方程的方法,掌握解方程的步骤与方法,根据方程的特点选择合适的方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.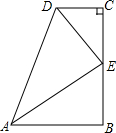 在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
 在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
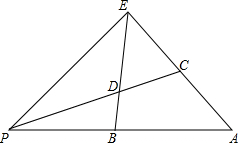 如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.
如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.
 张老师骑摩托车的速度为每小时45千米,学生步行的速度是每小时5千米,学校与车站相距15千米.如果2名学生要在55分钟内从学校到车站,请张老师用摩托车送,但摩托车后座只能坐一人,学生不能驾车,请你设计一个方案(学生只能步行或乘摩托车,上下摩托车的时间不计),使2名学生能在55分钟内全部到达车站,并用方程的有关知识说明理由.
张老师骑摩托车的速度为每小时45千米,学生步行的速度是每小时5千米,学校与车站相距15千米.如果2名学生要在55分钟内从学校到车站,请张老师用摩托车送,但摩托车后座只能坐一人,学生不能驾车,请你设计一个方案(学生只能步行或乘摩托车,上下摩托车的时间不计),使2名学生能在55分钟内全部到达车站,并用方程的有关知识说明理由.