题目内容
19.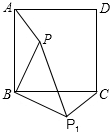 如图,点P是正方形ABCD内一点,将△ABP绕点B按顺时针方向旋转至与△CBP1重合,若PB=4cm,则PP1=4$\sqrt{2}$cm.
如图,点P是正方形ABCD内一点,将△ABP绕点B按顺时针方向旋转至与△CBP1重合,若PB=4cm,则PP1=4$\sqrt{2}$cm.
分析 由旋转的性质可知PB1=PB=4cm,∠ABP=∠CBP1,故此可知∠PBP1=90°,然后利用勾股定理可求得PP1=4$\sqrt{2}$cm.
解答 解:由旋转的性质可知:PB1=PB=4cm,∠ABP=∠CBP1.
∵∠ABP=∠CBP1,
∴∠PBP1=∠ABC=90°.
在Rt△PBP1中,由勾股定理得:PP1=$\sqrt{B{P}^{2}+B{{P}_{1}}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$cm.
故答案为:4$\sqrt{2}$cm.
点评 本题主要考查的是旋转的性质,由旋转的性质得到三角形PBP1为等腰直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.A、B两地相距870千米,有两列火车同时从两站相对开出,甲车每小时行60千米,乙车每小时比甲车快5千米,6小时后两车的距离为( )
| A. | 80千米 | B. | 90千米 | C. | 100千米 | D. | 120千米 |
 小明为自己是重庆一中的学子感到很自豪,他特制了一个写有“我爱重庆一中”的正方体盒子,其展开图如图所示,则原正方体中与“重”字所在的面相对的面上的字是中.
小明为自己是重庆一中的学子感到很自豪,他特制了一个写有“我爱重庆一中”的正方体盒子,其展开图如图所示,则原正方体中与“重”字所在的面相对的面上的字是中. 已知一次函数y=kx+b的图象如图所示,
已知一次函数y=kx+b的图象如图所示, 如图,∠ABD=∠BCD=90°,AB=4,sinA=$\frac{3}{5}$,CD=2,求∠CBD的三个三角函数值.
如图,∠ABD=∠BCD=90°,AB=4,sinA=$\frac{3}{5}$,CD=2,求∠CBD的三个三角函数值.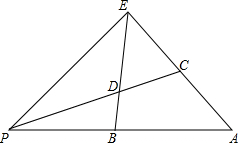 如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.
如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.