题目内容
11.若ax2+bx+1与2x2-3x+1的积不含x的一次项,不也含x的三次项,则a=2,b=3.分析 根据题意将两个多项式进行相乘化简即可求出答案.
解答 解:(ax2+bx+1)(2x2-3x+1)
=2ax4-3ax3+ax2+2bx3-3bx2+bx+2x3-3x+1
=2ax4-3ax3+2bx3+2x3+ax2-3bx2+bx-3x+1
=2ax4-(3a-2b-2)x3+(a-3b)x2+(b-3)x+1
由题意可知:$\left\{\begin{array}{l}{3a-2b-2=0}\\{b-3=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$
故答案为:2;3
点评 本题考查多项式乘以多项式,涉及二元一次方程的解法,注意不含某一项只需要令其系数为0即可.

练习册系列答案
相关题目
2.△ABC中,AB=13,BC=10,BC边上中线AP=12,则AB,AC关系为( )
| A. | AB>AC | B. | AB=AC | C. | AB<AC | D. | 无法确定 |
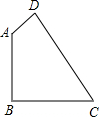 如图,四边形ABCD中,AB=BC=2,AD=1,CD=$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
如图,四边形ABCD中,AB=BC=2,AD=1,CD=$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.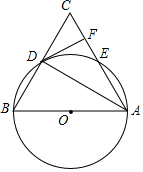 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.
如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.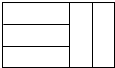 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是3 cm 2.
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是3 cm 2.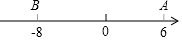 已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上两个动点,点M从A点出发向左运动,速度为每秒2个单位长度,与此同时,点N从B点出发向右运动,速度为M点的3倍,经过多长时间,点M与点N相距50个单位长度?这时点M、N所对应的数分别是多少?
已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上两个动点,点M从A点出发向左运动,速度为每秒2个单位长度,与此同时,点N从B点出发向右运动,速度为M点的3倍,经过多长时间,点M与点N相距50个单位长度?这时点M、N所对应的数分别是多少?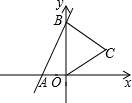 如图,直线y=3x+6与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为(-1,3).
如图,直线y=3x+6与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边△OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为(-1,3).