题目内容
20.抛物线y=ax2+bx+c(a≠0)的顶点在直线y=x上,将该抛物线沿直线y=x方向平移一定的距离后,再绕顶点旋转180°,最终得到的抛物线y=-3x2-12x-14与原抛物线关于原点中心对称.(1)求原抛物线的解析式及平移的距离;
(2)若1≤x≤5,求代数式$\frac{1}{a{x}^{2}+bx+c}$的最小值.
分析 (1)先确定抛物线y=-3x2-12x-14的顶点坐标,然后根据中心对称的性质求得原抛物线的顶点坐标,即可求得解析式;由顶点坐标得出顶点沿x轴的正方向平移2个单位,沿y轴的正方向平移2个单位,从而求得沿直线y=x方向平移的距离.
(2)求得当1≤x≤5时,函数y=3x2-12x+14的最大值,即可求得代数式$\frac{1}{a{x}^{2}+bx+c}$的最小值.
解答 解:(1)∵y=-3x2-12x-14=-3(x+2)2-2,
∴顶点为(-2,-2),
∵抛物线y=-3x2-12x-14与原抛物线关于原点中心对称,
∴原抛物线的顶点为(2,2),
∴原抛物线的解析式为y=3(x-2)2+2,
即y=3x2-12x+14.
由顶点坐标可知,顶点沿x轴的正方向平移2个单位,沿y轴的正方向平移2个单位,
∴沿直线y=x方向平移了4$\sqrt{2}$个单位.
(2)把x=1代入y=3x2-12x+14得,y=5,
把x=5代入y=3x2-12x+14得,y=29,
∴1≤x≤5时,函数y=3x2-12x+14的最大值为29,
∴代数式$\frac{1}{a{x}^{2}+bx+c}$的最小值为$\frac{1}{29}$.
点评 本题考查了二次函数图象与几何变换,一次函数图象上点的坐标特征,二次函数的最值以及中心对称的性质,得出顶点坐标是解题的关键.

练习册系列答案
相关题目
12.多项式5x2-8x+1+x2+7x-6x2是( )
| A. | 一次二项式 | B. | 二次六项式 | C. | 二次二项式 | D. | 二次三项式 |
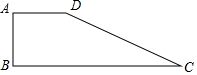 如图:四边形ABCD中,AB=4,BC=13,CD=12,AD=3,∠A=90°,求四边形ABCD的面积.
如图:四边形ABCD中,AB=4,BC=13,CD=12,AD=3,∠A=90°,求四边形ABCD的面积.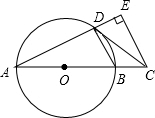 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
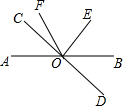 如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数.
如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数.