题目内容
16.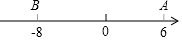 已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上两个动点,点M从A点出发向左运动,速度为每秒2个单位长度,与此同时,点N从B点出发向右运动,速度为M点的3倍,经过多长时间,点M与点N相距50个单位长度?这时点M、N所对应的数分别是多少?
已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上两个动点,点M从A点出发向左运动,速度为每秒2个单位长度,与此同时,点N从B点出发向右运动,速度为M点的3倍,经过多长时间,点M与点N相距50个单位长度?这时点M、N所对应的数分别是多少?
分析 首先设经过x秒点M与点N相距50个单位,根据题意可得等量关系:点M的运动路程+N的运动路程=14=50,根据等量关系列出方程,再解,然后可得x的值,进而可得点M、N所对应的数.
解答 解:设经过x秒点M与点N相距50个单位.
依题意可列方程为:2x+6x-14=50,
解方程,得x=8.
2x=16,16-6=10,即点M所对应的数是-10.
6x=48,48-8=40,即点N所对应的数是40.
答:经过8秒点M与点N相距50个单位,这时点M、N所对应的数分别是-10,40.
点评 此题主要考查了数轴,以及一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
6. 如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
 如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )| A. | $\sqrt{2014}$ | B. | $\sqrt{2015}$ | C. | $\sqrt{2016}$ | D. | $\sqrt{2017}$ |
7.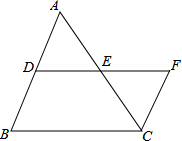 如图,D、E是△ABC的边AB、AC的中点,延长DE至F使EF=DE,则S△CFE:S四边形BCFD的值为( )
如图,D、E是△ABC的边AB、AC的中点,延长DE至F使EF=DE,则S△CFE:S四边形BCFD的值为( )
 如图,D、E是△ABC的边AB、AC的中点,延长DE至F使EF=DE,则S△CFE:S四边形BCFD的值为( )
如图,D、E是△ABC的边AB、AC的中点,延长DE至F使EF=DE,则S△CFE:S四边形BCFD的值为( )| A. | 1:3 | B. | 2:3 | C. | 1:4 | D. | 2:5 |
6.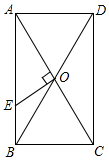 如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
 如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )| A. | AE=5 | B. | ∠BOE=∠BCE | C. | CE⊥OB | D. | sin∠BOE=$\frac{3}{5}$ |
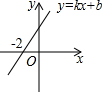 如图,一次函数y=kx+b的图象与x轴的交点坐标为(-2,0),则下列说法:
如图,一次函数y=kx+b的图象与x轴的交点坐标为(-2,0),则下列说法: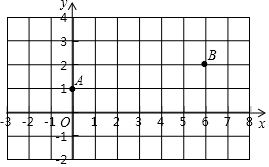 如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2.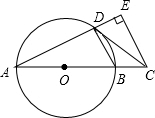 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.